Question

Число 9 представьте в виде суммы двух неотрицательных слагаемых так, чтобы произведение квадрата одного из них на утроенное другое слагаемое было наибольшим.

Answer 1

Для того, чтобы найти наибольшее значение произведения квадрата одного из них на утроенное другое слагаемое, составим функцию: пусть первое число будет х, а второе (9-х). Тогда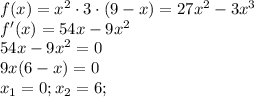 $f(x) = x^{2}\cdot3\cdot(9-x) = 27x^{2} -3x^{3}\\f'(x)=54x-9x^{2}\\54x-9x^{2}=0\\9x(6-x)=0\\x_{1}=0;x_{2}=6;$

Первое число не подходит по условию задачи, следовательно искомое число равно 6, а второе 9-6=3.

ответ искомые числа 6 и 3: 9 = 6 + 3;