ответ: 65 км/ч
Объяснение:
1) 312 : 2 = 156 (км) - половина расстояния
2) 12 мин = 12/60 ч = 1/5 ч
Скорость Время Расстояние
До остановки x - 5 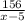 156
156
После ост. x 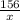 156
156
Время до остановки на 12 мин больше времени после остановки:
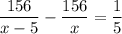
х > 5 по смыслу задачи, поэтому умножим обе части уравнения на
5x(x - 5):
780x - 780(x - 5) = x(x - 5)
780x - 780x + 3900 = x² - 5x
x² - 5x - 3900 = 0
По теореме Виета:
x₁ · x₂ = - 3900
x₁ + x₂ = 5
Значит, x₁ = - 60 - не подходит по смыслу задачи
x₂ = 65
ответ: 65 км/ч
z=ln(x+e^(-y))
dz/dx=1/(x+e^(-y))*(x+e^(-y))'=1/(x+e^(-y))
d2z/dx2=((x+e^(-y))^(-1))'=-(x+e^(-y))^(-2)*(x+e^(-y))'=-1/(x+e^(-y))^2
d3z/dx2dy=(-(x+e^(-y))^(-2))'=-(-2(x+e^(-y)))^(-3)*(x+e^(-y))'=2(x+e^(-y))^(-3)*(-e^(-y))=-2e^(-y)/(x+e^(-y))^3
dz/dy=1/(x+e^(-y))*(x+e^(-y))'=1/(x+e^(-y))*(-e^(-y))=-e^(-y)/(x+e^(-y))
d2z/dydx=(-e^(-y)*(x+e^(-y))^(-1))'=-e^(-y)*((x+e^(-y))^(-1))'=
-e^(-y)*(-((x+e^(-y))^(-2)))*(x+e^(-y))'=e^(-y)/(x+e^(-y))^2
d3z/dydx2=(e^(-y)/(x+e^(-y))^2)'=e^(-y)((x+e^(-y))^(-2))'=
e^(-y)*(-2((x+e^(-y))^(-3)))*(x+e^(-y))'=-2e^(-y)/(x+e^(-y))^3
и все
-2e^(-y)/(x+e^(-y))^3-(-2e^(-y)/(x+e^(-y))^3)=-2e^(-y)/(x+e^(-y))^3+2e^(-y)/(x+e^(-y))^3=0
Объяснение: