2. 10
3. В первом - 15, во втором - 45, в двух - 60.
4. Верно при любом значении x.
5. 44
Объяснение:
2.
Вся дорога - 26 мин.
Идет пешком - на 6 мин. дольше, чем едет на автобусе
Едет на автобусе - ? мин.
Пусть x - время, которое Таня едет на автобусе, тогда x + 6 - время, которое Таня идет пешком.
Составим уравнение:
x + 6 + x = 26
2x + 6 = 26
2x = 26 - 6
2x = 20
x = 10
ответ: Таня едет на автобусе 10 минут.
3.
1 сарай - в 3 раза больше сена, чем во 2.
2 сарай - ? тонн сена.
После того, как из первого сарая увезли 20 тонн сена, а во второй привезли 10 тонн сена, в обоих сараях сена стала поровну.
Сколько тонн сена было в двух сараях первоначально?
Пусть во втором сарае было x тонн сена, тогда в первом сарае было 3x тонн сена. Зная, что после того, как из первого сарая увезли 20 тонн, а в первый привезли 10 тонн, количество сена в сараях уровнялось, мы можем составить уравнение:
1) 3x - 20 = x + 10
3x - x = 10 + 20
2x = 30
x = 15 (тонн сена) - было во втором сарае
2) 3 * 15 = 45 (тонн сена) - было в первом сарае.
3) 15 + 45 = 60 (тонн сена)
ответ: первоначально в первом сарае было 45 тонн сена, во втором - 15 тонн сена, а в двух сараях - 60 тонн сена.
4.
7x - (x + 3) = 3(2x - 1)
7x - x - 3 = 6x - 3
7x - x = 6x
6x = 6x
Будет верно при любом значении x.
5.
Масса ящика с яблоками = 22кг +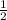 
его массы.
Масса ящика с яблоками - ?
Пусть x - масса ящика с яблоками, тогда x : 2 - половина массы.
Составим уравнение:
x = 22 + x : 2
x = 22 +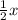 
2x = 44 + x
2x - x = 44
x = 44
ответ: масса ящика с яблоками - 44 кг.
Пусть сторона квадрата х см, тогда длина прямоугольника (3х) см, а ширина прямоугольника - (х - 5) см.
Т.к. площадь квадрата находят по формуле S = а², где а - сторона квадрата, о площадь данного квадрата равна (х²) см².
А т.к площадь прямоугольника находят по формуле S = a · b, где a и b - длина и ширина прямоугольника, то площадь данного прямоугольника будет равна S = 3х · (х - 5) = 3х² - 15х (см²).
Т.к. площадь квадрата на 50 см² меньше площади прямоугольника, то составим и решим уравнение:
3x² - 15х = x² + 50,
3x² - x² - 15x - 50 = 0,
2x² - 15x - 50 = 0,
D = (-15)² - 4 · 2 · (-50) = 225 + 400 = 625 ; √625 = 25,
x₁ = (15 + 25)/(2 · 2) = 40/4 = 10,
x₂ = (15 - 25)/(2 · 2) = -10·/4 = -2,5 - не подходит по условию задачи.
Значит, сторона квадрата равна 10 см.
ответ: 10 см.
ответ в закреплённом файле.