Сначала нужно выполнить чертеж (смотрите рисунок). Вообще говоря, при построении чертежа в задачах на площадь нас больше всего интересуют точки пересечения линий. Найдем точки пересечения параболы y=4-x² и прямой y=2-x. Это можно сделать двумя Первый это посмотреть на график где линии пересекаются, второй это аналитический В данном случае можно воспользоваться графическим так как на графике ясно видно, что парабола и прямая пересекаются в точке (-1 ; 3) и (2 ; 0).Но бывают случаи, когда точкой пересечения будет, например, точка (-3,14 ; 1), тогда графически вы не сможете определить точки пересечения, в таком случае используется аналитический метод. Попробуем применить аналитический для вычисления точек пересечения. Для этого мы приравниваем уравнения y=4-x² и y=2-x 4-x²=2-x x²-x+2-4=0 x²-x-2=0 применим теорему Виета для решения квадратного уравнения x₁+x₂=1 x₁x₂= -2 x₁=2 x₂= -1
Теперь посмотрим где расположена фигура. Нам важно, какой график выше (относительно другого графика), а какой – ниже.
Из графика видно, что выше расположена парабола y=4-x² , а ниже прямая y=2-x.
Формула для вычисления площади: где это функция которая расположена выше, чем функция
таким образом для исчисления площади нужно взять интеграл
ответ: площадь фигуры, ограниченной линиями у = 4 - х² и у = 2 - х равна 4,5
Пусть скорость первого пешехода - хскорость второго пешехода - увремя в пути обоих пешеходов 3ч 45 мин= 3,75чтогда первый пешеход успеет пройти расстояние 3,75х ,а второй 3,75 утогда 3,75 х+3,75у=30- первое уравнение Если первый выйдет на 2 часа раньше и будет идти ещё 2,5 часа то он успеет пройти расстояние 4,5х ,а второй выходит позднее и пройдёт 2.5 у Значит 4,5х+2,5у=30 второе уравнение системы Пусть скорость первого пешехода - хскорость второго пешехода - увремя в пути обоих пешеходов 3ч 45 мин= 3,75чтогда первый пешеход успеет пройти расстояние 3,75х ,а второй 3,75 утогда 3,75 х+3,75у=30- первое уравнение Если первый выйдет на 2 часа раньше и будет идти ещё 2,5 часа то он успеет пройти расстояние 4,5х ,а второй выходит позднее и пройдёт 2.5 у Значит 4,5x+2,5 у=30 второе уравнение системы
3,75x+3,75y=30 4,5x+2,5y=30 Первое уравнение умножить на 2,второе на (-3)получаем
7,5x+7,5y=60 -13,5x-7,5y=-90 Используем метод сложения и получаем-6х=-30х=-30:(-6)х=5 км/ч-скорость первого пешеходаПодставляем во второе уравнение системы4,5*5+2,5у=3022,5+2,5у=302,5у=30-22,52,5у=7,5у=7,5:2,5у=3 км/ч-скорость второго пешеходаответ 5 км/ч и 3 км/ч
Первый это посмотреть на график где линии пересекаются, второй это аналитический В данном случае можно воспользоваться графическим так как на графике ясно видно, что парабола и прямая пересекаются в точке (-1 ; 3) и (2 ; 0).Но бывают случаи, когда точкой пересечения будет, например, точка (-3,14 ; 1), тогда графически вы не сможете определить точки пересечения, в таком случае используется аналитический метод.
Попробуем применить аналитический для вычисления точек пересечения. Для этого мы приравниваем уравнения y=4-x² и y=2-x
4-x²=2-x
x²-x+2-4=0
x²-x-2=0
применим теорему Виета для решения квадратного уравнения
x₁+x₂=1
x₁x₂= -2
x₁=2
x₂= -1
Теперь посмотрим где расположена фигура. Нам важно, какой график выше (относительно другого графика), а какой – ниже.
Из графика видно, что выше расположена парабола y=4-x² , а ниже прямая y=2-x.
Формула для вычисления площади: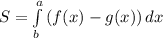 где
где  это функция которая расположена выше, чем функция
это функция которая расположена выше, чем функция 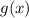
таким образом для исчисления площади нужно взять интеграл
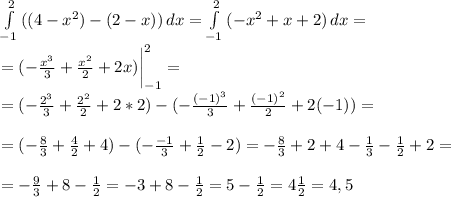
ответ: площадь фигуры, ограниченной линиями у = 4 - х² и у = 2 - х равна 4,5