Общее число возможных элементарных исходов равно числу которыми можно извлечь 3 шара из 8:
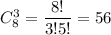
Количество благоприятных исходов:
а) Подсчитаем сколькими можно вынуть 3 красных шара.
это можно сделать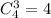 
Вероятность того, что все 3 шарика красные, равна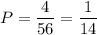 
б) Подсчитаем сколькими можно вынуть 2 шарика красного цвета и 1 желтого. Красных 2 шарика можно выбрать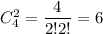 
а 1 желтого По правилу произведения, таких
Вероятность того, что среди выбранных 3 шаров будет 2 красного цвета и 1 желтого, равна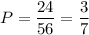 
в) Подсчитаем сколькими можно выбрать 3 шарика одного цвета. Три красных шара мы посчитали в пункте а таких 4, аналогично, выбрать три желтых шара можно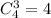 
По правилу сложения, таких
Вероятность того, что среди трех выбранных шаров будет все шарики одного цвета, равна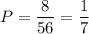 
Задать вопрос
Войти
АнонимМатематика09 ноября 14:55
Решите систему уравнений методом алгебраического сложения 2x^2+3y^2=14. -x^2+2y^2=7
ответ или решение1
Харитонова Светлана
Решим заданную систему уравнений методом алгебраического сложения:
2х^2 + 3у^2 = 14;
-х^2 + 2у^2 = 7.
1. Умножим второе уравнение на 2:
2х^2 + 3у^2 = 14;
-2х^2 + 4у^2 = 14.
2. Выполним прибавление первого и второго уравнения:
2х^2 - 2х^2 + 3у^2 + 4у^2 = 14 + 14;
7у^2 = 28;
у^2 = 28 : 7;
у^2 = 4;
у1 = 2;
у2 = -2.
3. Подставим значение у в первое уравнение и найдем значение х:
2х^2 + 3 * 2^2 = 14;
2х^2 + 3 * 4 = 14;
2х^2 + 12 = 14;
2х^2 = 14 - 12;
2х^2 = 2;
х^2 = 2 : 2;
х^2 = 1;
х1 = 1;
х2 = -1.
2х^2 + 3 * (-2)^2 = 14;
2х^2 = 14 - 12;
2х^2 = 2;
х^2 = 1;
х1 = 1;
х2 = -1.