№1 34,5; 35,1; 34,4; 34,2; 34,7; 34,6; 35,0; 34,2; 34,5; 34,8 найдите отклонения показаний от среднего значения. сколько показаний меньше, чем среднее? сколько показаний больше, чем среднее?

👇

Увидеть ответ

Ответ:

yanakuzmina1

04.12.2022

34,5; 35,1; 34,4; 34,2; 34,7; 34,6; 35,0; 34,2; 34,5; 34,8

34,2; 34,2 34,4 34,5 34,5; 34,6 34,7 34,8 35,0 35,1; ;

среднее 34,6 (Сумма всех 346:10=34,6)

Отклонения:

-0,4 -0,4 -0,2 -0,3 -0,3 0 0,1 0,2 0,4 0,5

Меньше среднего 5 показаний

Больше среднего 4 показания

4,5(14 оценок)

Открыть все ответы

Ответ:

Marina22111

04.12.2022

если $x< 0$ , то $2x< 0\; \; \rightarrow \; \; 2x-5< 0$ .

тогда модуль отрицательного выражения равен противоположному выражению и $|2x-5|=-(2x-5)=5-2x$ .

$(5-2x)'=5'-(2x)'=0-2=-2$

$(|2x-5|)'=-2$ при $x< 0$ .

при $x=0$ получим $(2x-5)\big |_{x=0}=-5$ , и тогда $(-5)'=0$ .

$x\in (-\infty ,0\, ]\, : \; \; (|2x-5|)'=\left \{ {{-2\; ,\; esli\; x< 0\, ,} \atop {0\; ,\; esli\; x=0\, .}} \right.$

4,7(88 оценок)

Ответ:

gree04

04.12.2022

Решение:

Немного теории. Систему уравнений можно записать в следующем виде:

A·x = b

где A - матрица коэффициентов, x - вектор-столбец переменных, b - вектор-столбец свободных членов.

Умножим эту систему на обратную матрицу коэффициентов A⁻¹ слева. Тогда:

A⁻¹·A·x = A⁻¹·b

x = A⁻¹·b

Таким образом, чтобы решить систему уравнений, нужно найти обратную матрицу коэффициентов и умножить ее на вектор-столбец свободных членов.

1) Обратная матрица

Будем искать обратную матрицу через алгебраические дополнения. Для начала найдем определитель матрицы A :

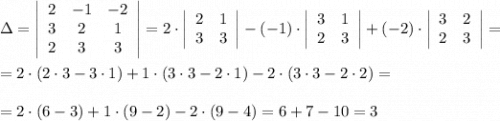
$\Delta =\left|\begin{array}{ccc}2&-1&-2\\3&2&1\\2&3&3\end{array}\right|=2\cdot \left|\begin{array}{cc}2&1\\3&3\end{array}\right|-(-1)\cdot \left|\begin{array}{cc}3&1\\2&3\end{array}\right|+(-2)\cdot \left|\begin{array}{cc}3&2\\2&3\end{array}\right|=\\\\=2\cdot(2\cdot3-3\cdot1)+1\cdot(3\cdot3-2\cdot1)-2\cdot(3\cdot3-2\cdot2)=\\\\=2\cdot(6-3)+1\cdot(9-2)-2\cdot(9-4)=6+7-10=3$

Найдем элементы матрицы алгебраических дополнений:

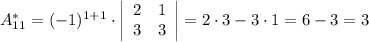
$A_{11}^{*}=(-1)^{1+1}\cdot \left|\begin{array}{cc}2&1\\3&3\\\end{array}\right|=2\cdot3-3\cdot1=6-3=3$

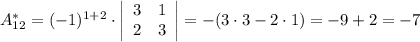
$A_{12}^{*}=(-1)^{1+2}\cdot \left|\begin{array}{cc}3&1\\2&3\\\end{array}\right|=-(3\cdot3-2\cdot1)=-9+2=-7$

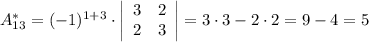
$A_{13}^{*}=(-1)^{1+3}\cdot \left|\begin{array}{cc}3&2\\2&3\\\end{array}\right|=3\cdot3-2\cdot2=9-4=5$

$A_{21}^{*}=(-1)^{2+1}\cdot \left|\begin{array}{cc}-1&-2\\3&3\\\end{array}\right|=-((-1)\cdot3-3\cdot(-2))=3-6=-3$

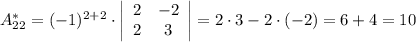
$A_{22}^{*}=(-1)^{2+2}\cdot \left|\begin{array}{cc}2&-2\\2&3\\\end{array}\right|=2\cdot3-2\cdot(-2)=6+4=10$

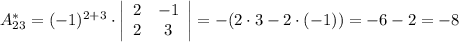
$A_{23}^{*}=(-1)^{2+3}\cdot \left|\begin{array}{cc}2&-1\\2&3\\\end{array}\right|=-(2\cdot3-2\cdot(-1))=-6-2=-8$

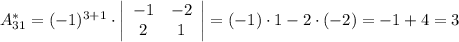
$A_{31}^{*}=(-1)^{3+1}\cdot \left|\begin{array}{cc}-1&-2\\2&1\\\end{array}\right|=(-1)\cdot1-2\cdot(-2)=-1+4=3$

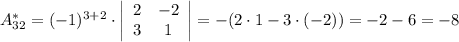
$A_{32}^{*}=(-1)^{3+2}\cdot \left|\begin{array}{cc}2&-2\\3&1\\\end{array}\right|=-(2\cdot1-3\cdot(-2))=-2-6=-8$

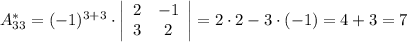
$A_{33}^{*}=(-1)^{3+3}\cdot \left|\begin{array}{cc}2&-1\\3&2\\\end{array}\right|=2\cdot2-3\cdot(-1)=4+3=7$

Тогда:

$A^*=\left(\begin{array}{ccc}3&-7&5\\-3&10&-8\\3&-8&7\end{array}\right)$

Транспонированная матрица алгебраических дополнений:

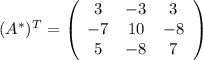
$(A^*)^T=\left(\begin{array}{ccc}3&-3&3\\-7&10&-8\\5&-8&7\end{array}\right)$

Обратная матрица:

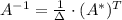
$A^{-1}=\frac{1}{\Delta} \cdot (A^*)^T$

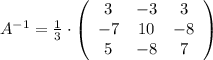
$A^{-1}=\frac{1}{3}\cdot \left(\begin{array}{ccc}3&-3&3\\-7&10&-8\\5&-8&7\end{array}\right)$

2) Вектор-столбец переменных

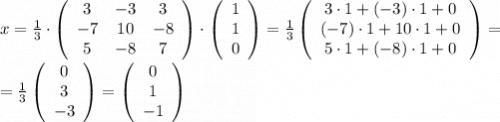
$x=\frac{1}{3}\cdot \left(\begin{array}{ccc}3&-3&3\\-7&10&-8\\5&-8&7\end{array}\right)\cdot\left(\begin{array}{ccc}1\\1\\0\end{array}\right)=\frac{1}{3} \left(\begin{array}{ccc}3\cdot1+(-3)\cdot1+0\\(-7)\cdot1+10\cdot1+0\\5\cdot1+(-8)\cdot1+0\end{array}\right)=\\\\=\frac{1}{3} \left(\begin{array}{ccc}0\\3\\-3\end{array}\right)=\left(\begin{array}{ccc}0\\1\\-1\end{array}\right)$