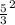Question

Сравните значения выражений
·$\frac{5}{3} ^{2}$ и 1,6⁰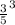

$\frac{3}5^{3 {$

Answer 1

Напомним основные свойства степени. Пусть а > 0, b > 0, n, m - любые действительные числа. Тогда

1) an am = an+m

2)

a

n

a

m

=

a

n

−

m

3) (an)m = anm

4) (ab)n = an bn

5)

(

a

b

)

n

=

a

n

b

n

6) an > 0

7) an > 1, если a > 1, n > 0

8) an < am, если a > 1, n < m

9) an > am, если 0< a < 1, n < m

В практике часто используются функции вида y = ax, где a - заданное положительное число, x - переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.

Определение. Показательной функцией называется функция вида y = ax, где а — заданное число, a > 0,

a

≠

1

Показательная функция обладает следующими свойствами

1) Область определения показательной функции — множество всех действительных чисел.

Это свойство следует из того, что степень ax где a > 0, определена для всех действительных чисел x.

2) Множество значений показательной функции — множество всех положительных чисел.

Чтобы убедиться в этом, нужно показать, что уравнение ax = b, где а > 0,

a

≠

1

, не имеет корней, если

b

≤

0

, и имеет корень при любом b > 0.

3) Показательная функция у = ax является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 < a < 1.

Это следует из свойств степени (8) и (9)

Построим графики показательных функций у = ax при a > 0 и при 0 < a < 1.

Использовав рассмотренные свойства отметим, что график функции у = ax при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.

Если х < 0 и |х| увеличивается, то график быстро приближается к оси Oх (но не пересекает её). Таким образом, ось Ох является горизонтальной асимптотой графика функции у = ax при a > 0.

Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.

График функции у = ax при 0 < a < 1 также проходит через точку (0; 1) и расположен выше оси Ох.

Если х > 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.

Если х < 0 и |х| увеличивается, то график быстро поднимается вверх.