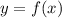 , когда a)
, когда a)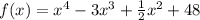
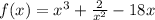
Дано неравенство ((2x-3) / (x^2+2x)) > 0,125 или ((2x-3) / (x^2+2x)) > 1/8.
Умножим обе части на 8: (16x - 24) / (x^2+2x) > 1.
По свойству дроби числитель больше знаменателя:
(16x - 24) > (x^2+2x). Перенесём левую часть вправо.
Получим равносильное неравенство x^2 + 2x - 16х + 24 < 0 или
x^2 - 14х + 24 < 0. Д = 196 - 4*24 = 100.
х1 = (14 + 10)/2 = 12, х2 = (14 - 10)/2 = 2.
Исходное неравенство можно представить так:
(х - 12)(х - 2)/(х(х + 2)) < 0.
Используем метод интервалов: -2 0 2 12
+ - + - +
Отсюда ответ: -2 < x < 0; 2 < x < 12.
Дано неравенство ((2x-3) / (x^2+2x)) > 0,125 или ((2x-3) / (x^2+2x)) > 1/8.
Умножим обе части на 8: (16x - 24) / (x^2+2x) > 1.
По свойству дроби числитель больше знаменателя:
(16x - 24) > (x^2+2x). Перенесём левую часть вправо.
Получим равносильное неравенство x^2 + 2x - 16х + 24 < 0 или
x^2 - 14х + 24 < 0. Д = 196 - 4*24 = 100.
х1 = (14 + 10)/2 = 12, х2 = (14 - 10)/2 = 2.
Исходное неравенство можно представить так:
(х - 12)(х - 2)/(х(х + 2)) < 0.
Используем метод интервалов: -2 0 2 12
+ - + - +
Отсюда ответ: -2 < x < 0; 2 < x < 12.
Объяснение: