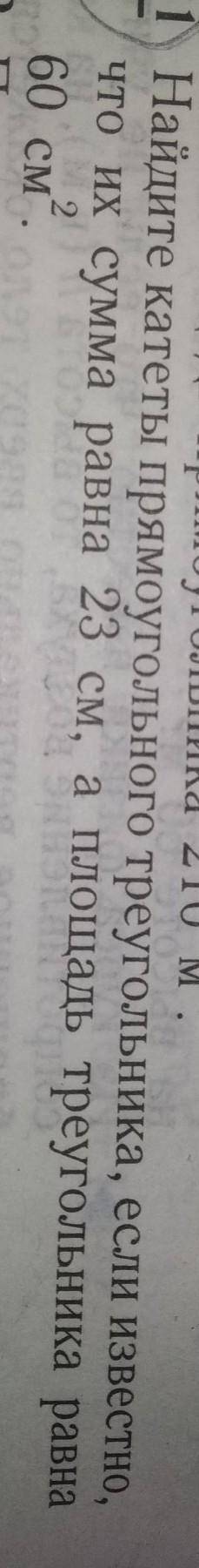
8см, 15см
Объяснение:
пусть катет АС=х, а катет ВС=23–х.
Поскольку площадь треугольника 60см², то она вычисляется по формуле:
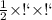
тогда:
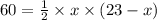
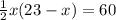
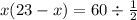
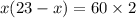
23x–x²=120
–x²+23x–120=0 |×(–1)
x²–23x+120=0
D= b²–4×ac=23²–4×1×120=529–480=49
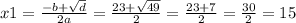
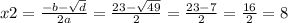
Тогда АС1=15см, или АС2=8см,
ВС1=23–15=8см
ВС2=23–8=15см
Итак: катеты в треугольнике составляют 8см и 15см

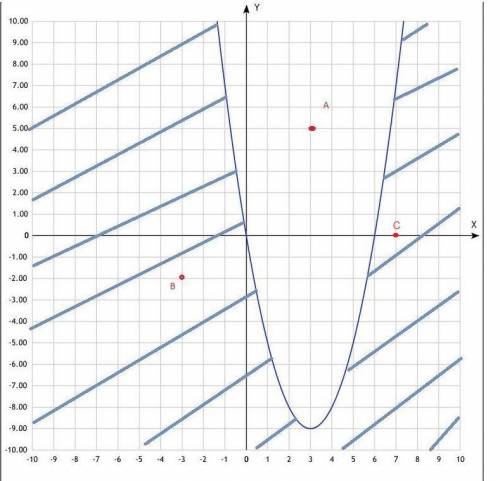
судя по заданию-график построен y=x^2-6x
решением неравенства
y<=x^2-6x- будет внешняя часть параболы, включая саму параболу. Если вы затрудняетесь с ее определением-совет: берите точку C (7;0) и подставляйте в неравенство
0<=49-42-верно. значит внешняя часть параболы, куда входит C (7;0)-решение. Сама парабола тоже решение- так как неравенство нестрогое. Область решения неравенства выделили штриховкой . как показано на чертеже.
По поводу точек А и В -поставлю их в плоскости рисунка.
А входит во внутреннюю область параболы-значит не является решением, В-во внешнюю, область штриховки, значит решение неравенства.
Катеты равны 8 см и 15 см.
Объяснение:
Пусть a и b -- катеты прямоугольного треугольника. Тогда по условию:
a + b = 23
ab / 2 = 60
Выразим b через a из первого уравнения: b = 23 – a. Подставим получившееся значение во второе уравнение:
a(23 – a) / 2 = 60
a(23 – a) = 120
23a – a² = 120
a² – 23a + 120 = 0
D = 23² – 4·120 = 49 = 7²
a₁ = (23 – 7) / 2 = 8 ⇒ b₁ = 23 – 8 = 15
a₂ = (23 + 7) / 2 = 15 ⇒ b₂ = 23 – 15 = 8
Полученные решения совпадают с точностью до перестановки катетов местами.