пусть ширина поля х м, тогда длина поля (х+31) м
S=a*b, где а и b стороны прямоугольника Площадь поля равна x*(x+31) м^2, что по условию задачи составляет 1830 м^2
Составим уравнение x(x+31)=1830
x^2+31x-1830=0
D=8281
x1=30
x2=-61 не подходит
ширина=30 м
длина=61 м
Проверка S=61*30=1830(м^2)
ответ:Скорость реки: 1 км/ч,
Скорость катера: 19 км/ч
Объяснение:
Скорость катера по течению за 15 мин= 5÷0,25(15 мин = 0,25 ч) =20 км/ч. Находим время за которое катер проходит 15 км по течению: 15÷20=0,75 ч. Общее время: 1+45÷60=1,75 ч. Значит, время против течения: 1,75-0,75=1. Находим скорость катера против течения реки: 18÷1=18км/ч. Далее мы берём скорость реки за Х. У нас получается уравнение:
20(км/ч) - 18(км/ч)=2Х
2=2Х
Х=1(км/ч)
Через скорость реки можно найти скорость катера 2-мя
1)20-1=19
2)18+1=19
Остается только оформить задачу как просит Ваш учитель.
Удачи)))
Пусть х км/ч собственная скорость катера (ОДЗ x>0)
у км/ч скорость течения реки (ОДЗ y>0),
тогда
(х+у) км/ч скорость катера по течению
(х-у) км/ч скорость катера против течения
По условию 15 км по течению и 18 км против течения пройдено за 1 ч 45 мин., иначе 1ч 45 мин = 1 ³/₄ часа,
Получаем первое уравнение:

По условию 5 км по течению катер проходит 15 мин., иначе 15 мин = ¹/₄ часа,
Получаем второе уравнение:

Система уравнений:

Решаем её.
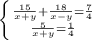
Из второго уравнения выразим (x+y):
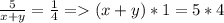

Подставим в первое:
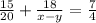
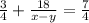
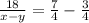
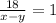

Решаем упрощенную систему:

Сложим:
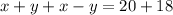
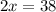
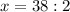
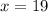
тогда
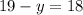
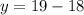

ответ: 19 км/ч собственная скорость катера;
1 км/ч скорость течения реки
Хм. Пусть x-длина поля, тогда x-31 - ширина поля.
Составим и решим уравнение:
x(x-31)=1830
x^2-31x=1830
x^2-31x-1830=0
D=b^2-4ac=961-4*1*(-1830)=8281
x1= (-b)-sqrt(D)/(2a)= 31-91/2=-30
x2= (-b)+sqrt(D)/(2a)= 31+91/2=61
длина поля = 61м.
ширина поля = 61-31=30м.
ответ: длина поля=61м, а ширина поля=30м.
[sqrt(D) - корень из (D)]