метод замены переменных и другие решения систем уравнений с двумя переменными. то что написано на доске желательно решить все то что на листочке написано нудно решить после слов "дома:"
Пусть первое число х, тогда второе число на у больше первого,а третье число больше второго так же на у. 1число-х 2число-х+y 3число-х+2у По условию задачи произведение первого числа на третье,меньше квадрата второго на 49. Составим уравнение: (x+y)^2-x(x+2y)=49 x^2+2xy+y^2-x^2-2xy=49 y^2=49 y1=7 y2= -7 По условию задачи даны натуральные числа,поэтому у2 не удовлетворяет условию задачи. Значит второе число больше первого на 7, а третье число,которое является наибольшим числом на 14 больше первого числа,которое является наименьшим. Т.е. наименьшее число меньше наибольшего на 14.
Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t)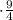 - объем работы системы из двух насосов за 2ч 15мин.
- объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение:
9t = 1
Значит,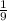 - цис./ч - производительность "медленного" насоса.
- цис./ч - производительность "медленного" насоса.
Тогда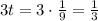 - цис./ч - производительность "быстрого" насоса.
- цис./ч - производительность "быстрого" насоса.
Следовательно,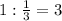 ч - потребуется "быстрому" насосу на заполнение цистерны.
ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.