для решения данного мы должны выяснить проходит ли график функции через точку с.
график функции
для того, чтобы выяснить проходит ли график функции через точку не обязательно выполнять построение графика. график функции проходит через точку, если координаты этой точки обращают формулу функции в верное числовое равенство. записи, в которых используется знак равно, разделяющий два объекта (два числа, выражения и т. называют равенствами. для того, чтобы выяснить проходит ли график функции через точку нужно:
подставить в формулу функции вместо у ординату точки с.
подставить в формулу функции вместо х абсциссу точки с.
если получится верное числовое равенство, точка лежит на графике.
вычислим принадлежит ли графику функции точка
график функции проходит через точку с, если их координаты обращают формулу y = -2x + 4 в верное числовое равенство. координаты точки с (20; -36), где абсцисса, то есть х =20, а ордината, то есть у = -36. подставим значения в формулу y = -2x + 4.
-36 = -2 * 20 + 4;
-36 = -40 + 4;
-36 = -36.
при умножении отрицательного числа на положительное мы получаем отрицательный результат.
так как обе части равны, значит мы получили верное равенство. следовательно точка с (20; -36) проходит через график функции y = -2x + 4.
a) Так как парабола проходит через эти точки, то говоря простым языком, они лежат на параболе.
Берете эти координаты точек и подставляете в ваше уравнение.
Напомню, что первая координата это x, а вторая y
A(-3; 7)
Первое уравнение относительно p и q
7 = (-3)^2 - 3p + q
2 - 3p + q = 0
B(1; 5)
Второе уравнение
5 = 1 + p + q
p + q - 4 = 0
В итоге мы получили два уравнения с двумя неизвестными, решаем нашу систему
2 - 3p + q = 0
p + q - 4 = 0
Из первого уравнения вычтем второе, получим
6 - 4p = 0 ⇒ p = 3/2
Тогда q = 5/2
b) тот же самый принцип
2 = 25 + 5p + q ⇒ 5p + q + 23 = 0
3 = 4 - 2p + q ⇒ -2p + q + 1 = 0
7p + 22 = 0 ⇒ p = -22/7
q = -51/7
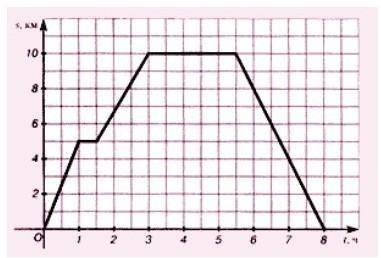
v=s/t= 10км/2.5часа=4 км/ч