Question

Номер 5.1, 5.3 найти значение выражения!

Answer 1

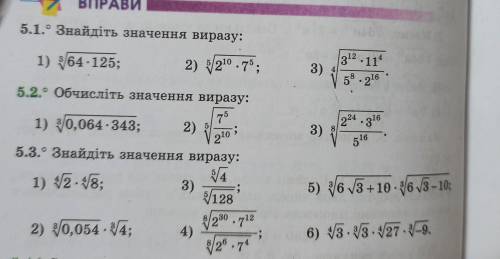
$5.1)\sqrt[3]{64*125}=\sqrt[3]{4^{3}*5^{3}}=4*5=\boxed{20}\\\\\sqrt[5]{2^{10}*7^{5}}=\sqrt[5]{(2^{2})^{5}*7^{5}}=2^{2}*7=4*7=\boxed{28}\\\\\sqrt[4]{\frac{3^{12}*11^{4}}{5^{8}*2^{16}}}=\sqrt[4]{\frac{(3^{3})^{4}*11^{4}}{(5^{2})^{4}*(2^{4})^{4}}}= \frac{3^{3}*11 }{5^{2}*2^{4}}=\frac{27*11}{25*16}=\frac{297}{400}=\boxed{0,7425}$

$5.3)\sqrt[4]{2}*\sqrt[4]{8}=\sqrt[4]{2*8}=\sqrt[4]{16}=\sqrt[4]{2^{4}}=\boxed2\\\\\sqrt[3]{0,054}*\sqrt[3]{4}=\sqrt[3]{0,054*4}=\sqrt[3]{0,216} =\sqrt[3]{0,6^{3}}=\boxed{0,6}\\\\\frac{\sqrt[5]{4}}{\sqrt[5]{128}}=\sqrt[5]{\frac{4}{128}}=\sqrt[5]{\frac{1}{32}}=\sqrt[5]{(\frac{1}{2})^{5}}=\boxed{0,5}$

$\frac{\sqrt[8]{2^{30}*7^{12}}}{\sqrt[8]{2^{6}*7^{4}}}=\sqrt[8]{\frac{2^{30}*7^{12}}{2^{6}*7^{4}}}=\sqrt[8]{2^{24}*7^{8}}=\sqrt[8]{(2^{3})^{8}*7^{8}}=2^{3}*7=8*7=\boxed{56}\\\\\sqrt[3]{6\sqrt{3} +10} *\sqrt[3]{6\sqrt{3}-10 } =\sqrt[3]{(6\sqrt{3}+10)(6\sqrt{3}-10)} =\\\\=\sqrt[3]{(6\sqrt{3})^{2}-10^{2}}=\sqrt[3]{108-100}=\sqrt[3]{8}=\sqrt[3]{2^{3}}=\boxed2$

$\sqrt[4]{3}*\sqrt[3]{3}*\sqrt[4]{27}*\sqrt[3]{-9} = \sqrt[4]{3*27}*\sqrt[3]{3*(-9)} =\sqrt[4]{3^{4}}*\sqrt[3]{(-3)^{3}} =3*(-3)=\boxed{-9}$

Answer 2

В 5.3 в 5 примере видимо опечатка, тк пример получается с большой иррациональностью