ответить на следующие вопросы, если точки A, B и C являются вершинами треугольника:
a) Найти уравнение стороны AB треугольника;
b) Найти уравнение высоты CK;
c) Найти уравнение медианы AN;
d) Найти точку пересечения высоты CN и медианы AN;
e) Составить уравнение прямой,проходящей через точку C и
параллельной стороне AB;
f) Найти расстояние от точки C до прямой AB.

A(1;3), B(-1;4), C(-2;-3)

👇

Увидеть ответ

Открыть все ответы

Ответ:

Alexkusaiko

31.01.2020

1) −0,8z5(1,2m5−2,5z) = -0.96z5m5+2z6

2) 11p3d(d3p−d3)=11p4d4−11p3d4

3) x9y2z(x2+10y2+7z2)=)x11y2z+10x9y4z+7x9y2z3

4) (4a3−3b)⋅2b−3b⋅(14a3−4b)=8a³b-6b²-42a³b+12b²= -34a³b+6b²

5) −9t2(2t5−3k)+5(4t7−2k)=-18t7+27t²k+20t7-10k=2t7+27t²k-10k

6) 13ab(14a²−b2)+14ab(b²−13a²)=182a³b-13ab³+14ab³=182a³b=ab³

10*(-2)³=10*(-8)=-80

7) 0,8(4a+3b)−6(0,3a+0,8b)=3.2a+2.4b-1.8a-4.8b=1.4а-2.4b

1.4*2-2.4*(-4)=2.8+9.6=12.4

8) 3x−ay+bz=3*(5с3+2)-3с(6с2-с+14)+15с3*(5с-1)=15с3+6-18с3+3с2-42с+75с4-15с3=75с4+(-18с3)+3с2+(-42с)+6

Объяснение:

4,7(86 оценок)

Ответ:

vihfdif23759Andr4675

31.01.2020

$2cosx\cdot sinx=\sqrt2\cdot cosx$

Если уравнение делить на cosx, то надо оговориться, что 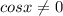$cosx\ne 0$ , так как на 0 делить нельзя. В силу этого можно потерять корни уравнения, при которых cosx обращается в 0, это 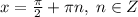$x=\frac{\pi}{2}+\pi n,\; n\in Z$ . Тогда надо отдельно проверить, не являются ли 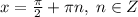$x=\frac{\pi}{2}+\pi n,\; n\in Z$ корнями заданного уравнения, подставив их в это уравнение.

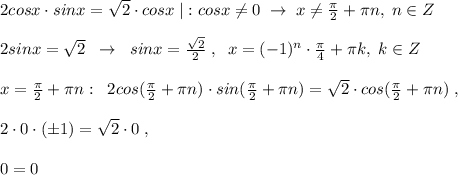
$2cosx\cdot sinx=\sqrt2\cdot cosx\; |:cosx\ne 0\; \to \; x\ne \frac{\pi }{2}+\pi n,\; n\in Z\\\\2sinx=\sqrt2\; \; \to \; \; sinx=\frac{\sqrt2}{2}\; ,\; \; x=(-1)^{n}\cdot \frac{\pi}{4}+\pi k,\; k\in Z\\\\x=\frac{\pi}{2}+\pi n:\; \; 2cos(\frac{\pi}{2}+\pi n)\cdot sin(\frac{\pi}{2}+\pi n)=\sqrt2\cdot cos(\frac{\pi}{2}+\pi n)\; ,\\\\2\cdot 0\cdot (\pm 1)=\sqrt2\cdot 0\; ,\\\\0=0$

Так как получили верное равенство, то 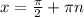$x=\frac{\pi}{2}+\pi n$ являются корнями заданного уравнения.

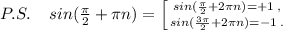
$P.S.\; \; \; \; sin(\frac{\pi}{2}+\pi n)=\left [ {{sin(\frac{\pi}{2}+2\pi n)=+1\; ,} \atop {sin(\frac{3\pi}{2}+2\pi n)=-1\; .}} \right.$

Чтобы не проводить лишнюю проверку , при решении уравнения надо просто вынести общий множитель cosx за скобку, тогда сразу получим две серии решений:

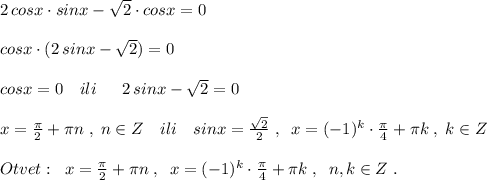
$2\, cosx\cdot sinx-\sqrt2\cdot cosx=0\\\\cosx\cdot (2\, sinx-\sqrt2)=0\; \; \Rightarrrow \\\\cosx=0\quad ili\quad \; \; 2\, sinx-\sqrt2=0\\\\x=\frac{\pi }{2}+\pi n\; ,\; n\in Z\quad ili\quad sinx=\frac{\sqrt2}{2}\; ,\; \; x=(-1)^{k}\cdot \frac{\pi}{4}+\pi k\; ,\; k\in Z\\\\Otvet:\; \; x=\frac{\pi }{2}+\pi n\; ,\; \; x=(-1)^{k}\cdot \frac{\pi}{4}+\pi k\; ,\; \; n,k\in Z\; .$