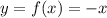 , x∈[-π;3]
, x∈[-π;3]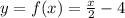 , x∈[0;4]
, x∈[0;4]2. первый член 12, знаменатель 6/12=1/2,
Энный член геометрической прогрессии ищем по формуле bn=b₁*qⁿ⁻¹
b₇=b₁*q⁷⁻¹=b₁*q⁶;
b₇=12*(1/2)⁶=12/64=3/16;
2. b₈=b₁*q⁷=14;
b₁₀=b₁*q⁹=126; разделим b₁₀/b₈=q²=9; q=±3; b₁=14/(±3)⁷=±14/3⁷, используем характеристическое свойство геометрической прогрессии, найдем b₉²=b₈*b₁₀,
b₉²=b₈*b₁₀=126*14;
значит, b₉=±14*3=±42
S₇=b₁*(q⁷-1)/(q-1)
если q=3, S₇=(14/3⁷)*(3⁷-1)/(3-1)=14*2186*/(2*2187)=7*2186*/2187=15302/2187
6 2180/2187
если q=-3, то S₇=
(-14/3⁷)*((-3)⁷-1)/(-3-1)=-14*2188*/(4*2187)=-7*2188*/(2*2187)=-1094*7/2187=
-7658/2187=-3 1097/2187
4. 4.(5)=4+05555=4+0.5+0.05+0.005+...
q=0.05/0.5=0.1
s=0.5/(1-0.1)=5/9
4.(5)=4+(5/9)=4 5/9
В решении.
Объяснение:
Решить уравнение:
2x²/(x-2) + (3x+2)/(2-x) = x
Сначала преобразовать знаменатель второй дроби, чтобы найти общий знаменатель:
(3x+2)/(2-x) = (3х+2)/ - (х-2) = - (3х+2)/(х-2), тогда уравнение примет вид:
2x²/(x-2) - (3x+2)/(х-2) = x
Умножить уравнение (все части) на (х-2), чтобы избавиться от дробного выражения:
2х² - (3х + 2) = х(х - 2)
Раскрыть скобки:
2х² - 3х - 2 = х² - 2х
Привести подобные члены:
2х² - 3х - 2 - х² + 2х = 0
х² - х - 2 = 0, квадратное уравнение, ищем корни:
D=b²-4ac =1 + 8 = 9 √D= 3
х₁=(-b-√D)/2a
х₁=(1 - 3)/2
х₁= -2/2
х₁= -1;
х₂=(-b+√D)/2a
х₂=(1 + 3)/2
х₂=4/2
х₂=2.
Так как х в знаменателе, по ОДЗ х не может быть равен 2, так как в этом случае знаменатель будет равен нулю, а дробь не будет иметь смысла. Значит, решение уравнения только х= -1.
с)
Функция у = - х - линейная. Так как к = - 1, - 1 < 0, то функция является убывающей на всей области определения.
Своего наибольшего значения на [-π;3] она будет достигать при наименьшем значении аргумента , т.е. при х = - π.
у = π - наибольшее значение функции.
Своего наименьшего значения на [-π;3] она будет достигать при наибольшем значении аргумента , т.е. при х = 3.
у = - 3 - наименьшее значение функции.
d) y = x/2 - 4 - линейная. Так как к = 1/2, 1/2 > 0, то функция является возрастающей на всей области определения.
При х = 4 функция будет достигать наибольшего значения:
у = 4/2 - 4 = -2;
у = - 2 - наибольшее значение функции.
При х = 0 функция будет достигать наименьшего значения:
у = 0/2 - 4 = -4;
у = - 4 - наименьшее значение функции.