,
, a 
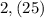
целая часть. У нас она равна 2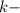
- количество цифр в периоде. У нас их 2
количество цифр до периода. У нас их 0
все цифры, включая период, в виде натурального числа. У нас это 25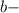
все цифры без периода в виде натурального числа. Их нет.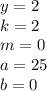
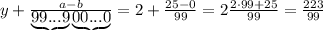
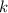подставляется количество 9, а под 
-количество нулей. У нас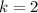 
, значит пишем две цифры 9, а 
, значит, нулей не пишем вообще. Между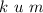 
не стоит знак умножения
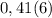
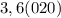
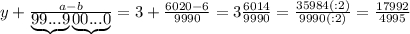
Любая сторона треугольника меньше суммы двух других его сторон.
Обозначим а - боковая сторона, с - основание.
1) Пусть а = 2 см и с = 5 см.
Должно выполняться неравенство: с < 2а.
5 < 2 · 2 - неверно.
Значит боковая сторона 5 см, основание 2 см.
2) Если а = 9 см и с = 21 см, то неравенство
21 < 2 · 9 - неверно.
Значит 21 см - боковая сторона, 9 см - основание.
3) Если а = 3 дм и с = 6 дм, то неравенство
6 < 2 · 3 - неверно.
Значит 6 дм - боковая сторона, 3 см - основание.
Объяснение: