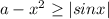
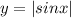расположен выше оси ОХ. 
.
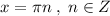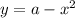- это параболы , ветви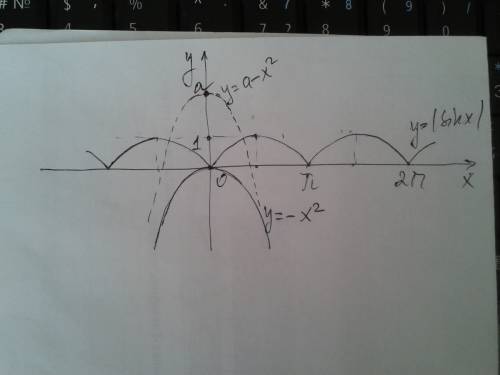
Пусть А - событие, которое состоится, если наудачу взятое двузначное число кратно 2, а В - событие, которое состоится, если это число кратно 7. Надо найти Р(А + В).Так как А и В - события совместные, то:
Р(А + В) = Р(А) + Р(В) - Р(АВ).
Двузначные числа - это 10, 11, . . . ,98, 99.
Всех их- 90 элементарных исходов. Очевидно, 45 из них кратны 2 (благоприятствуют наступлению А),
13 кратны 7 (благоприятствуют наступлению В) и ,наконец,7 кратны и 2, и 7 одновременно (благоприятствуют наступлению А×В). Далее по классическому определению вероятности:
Р(А) = 45/90 Р(В) = 13/90 Р(А×В) = 7/90
и, следовательно:
Р(А + В) = 45/90 + 13/90 - 7/90 = 51/90
ответ: 51/90
Объяснение:
-m(m+2)+(m+3)(m-3) = -m²-2m+m²-9 = -2m-9 = -2*0.5-9 = -10
-p(p+4)+(p-2)(p+2) = -p²-4p+p²-4 = -4p-4 = -4*(3/4)-4 = -3-4= -7
-x(x+2)+(x+5)^2 = -x²-2x+x²+10x+25 = 8x+25 = 8*(-3/8)+25 = -3+25=22
-c(c+3)+(c+4)^2 = -c²-3c+c²+8c+16 = 5c+16 = 5*(-2/5)+16 = -2+16=14