а)
При -2<x≤2, графиком функции f(x) будет y=3-x². Это парабола, ветви направлены вниз, координата вершины (0;3). Найдём точки пересечения с осями координат:
x=0 ⇒ y=3-0²=3; (0;3)
y=0 ⇒ 3-x²=0; x²=3; x=±√3; (-√3;0), (√3;0).
Всё, что мы нашли находится в указанном промежутке. 3-(-2)²=3-2² - ординаты границ промежутка совпадают, период равен 4 ⇒ 2-4 = -2, поэтому график функции f(x) будет непрерывным. Таблицу точек для y=3-x² и график функции смотри в приложении.
б)
Нули для y=3-x² мы знаем, для f(x) будут такие же нули, но есть ещё период, поэтому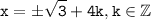 
- ответ.
в)
Определим по графику.
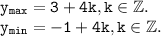
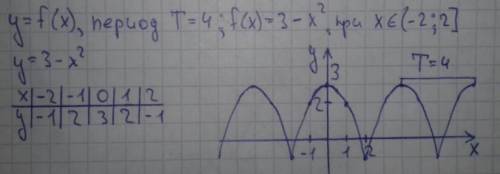
функция задана формулой у=18-2х^2. Не выполняя построения определите
а) координаты точек пересечения графика функции с осями координат
Пересечение в осью Ох: у=0
18-2x²=0
2x²=18
x²=9
x=3 или x=-3
точки пересечения (3;0) или (-3;0)
Пересечение с осью Оу: х=0
18-2*0=18
Точка пересечения (0;18)
б)значение функции если значение аргумента равно 2
18-2*2²=18-2*4=18-8=10
Значение функции y(2)=10
в)значение аргумента, при котором значение функции равно 16
18-2x²=16
2x²=2
x²=1
x=1 или х= -1
г)проходит ли график функции через точку В (-2: 10)
х=-2 у=10
18-2*(-2)²=18-2*4=18-8=10
Да, проходит
2
функция задана формулой у=2х^2-8 . Не выполняя построения определите
а) координаты точек пересечения графика функции с осями координат
пересечение с осью Ох: у=0
2x²-8=0
2x²=8
x²=4
x=2 или х=-2
Точки пересечения (2;0) или (-2;0)
пересечение с осью Оу: х=0
2*0-8= -8
Точка пересечения (0;-8)
б)значение функции если значение аргумента равно 3
у(3)=2*3²-8=2*9-8=18-8=10
в)значение аргумента, при котором значение функции равно -6
2x²-8= -6
2x²=2
x²=1
x=1 или х= -1
г)проходит ли график функции через точку А( -3:10)
х= -3 у=10
2*(-3)²-8=2*9-8=18-8=10
Да, проходит