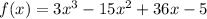
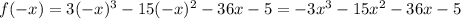
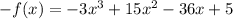
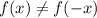 и
и 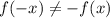 , то функция является функцией общего вида.
, то функция является функцией общего вида.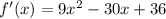
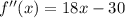
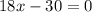
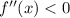
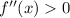
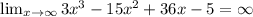
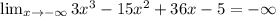
1)Решение системы уравнений (-1; 10);
2)Решение системы уравнений (4; -1)
Объяснение:
Решите систему уравнений методом сложения:
1)y-6x=16
4y+6x=34
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, чтобы коэффициенты при неизвестном каком-то были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают уравнения, можно умножать обе части уравнения на одно и то же число, делить.
В данной системе ничего преобразовывать не нужно, коэффициенты при х одного значения и с противоположными знаками:
Складываем уравнения:
у+4у-6х+6х=16+34
5у=50
у=10
Теперь подставляем значение у в любое из двух уравнений системы и вычисляем х:
y-6x=16
-6х=16-у
-6х=16-10
-6х=6
х=6/-6
х= -1
Решение системы уравнений (-1; 10)
2)3x-4y=16
5x+6y=14
В данной системе, чтобы применить метод сложения, нужно первое уравнение умножить на 3, второе на 2:
9х-12у=48
10х+12у=28
Складываем уравнения:
9х+10х-12у+12у=48+28
19х=76
х=76/19
х=4
Теперь подставляем значение х в любое из двух уравнений системы и вычисляем у:
3x-4y=16
-4у=16-3*4
-4у=16-12
-4у=4
у=4/-4
у= -1
Решение системы уравнений (4; -1)
5 см и 8 см - стороны прямоугольника
Объяснение:
Р = 2(а+в) = 26 см - периметр прямоугольника
S1 = а² см² - площадь первого квадрата
S2 = в² см² - площадь второго квадрата
Составляем систему уравнений:
2(а+в) = 26
а² + в² = 89
2(а+в) = 26
а+в = 13
а = 13 - в - подставим это значение а во второе уравнение
а² + в² = 89
(13-в)² + в² = 89
169 - 26в + в² + в² = 89
2в² - 26в +169 - 89 = 0
2в² - 26в + 80 = 0 - разделим все уравнение на 2
в² - 13в + 40 = 0
в² - 8в - 5в + 40 = 0
в(в-8) - 5(в-8) = 0
(в-5)(в-8) = 0
Если в=5 см, то а=8 см, или наоборот в=8, а=5
ответ: 5 см и 8 см - стороны прямоугольника