Пусть a - одно число. Тогда два других будут равны (a + 1) и (a + 2). Зная, что сумма квадратов данных чисел равна 1589, получим уравнение: a² + (a + 1)² + (a + 2)² = 1589 a² + a² + 2a + 1 + a² + 4a + 4 = 1589 3a² + 6a + 5 = 1589 3a² + 6a - 1584 a² + 2a - 528 = 0 a² + 2a + 1 - 529 = 0 (a + 1)² - 23² = 0 (a + 1 - 23)(a + 1 + 23) = 0 a = 22 и a = -24 a = -24 не уд. условию задачи (число натуральное). Значит, наименьшее из чисел равно 22. 1) 22 + 1 = 23 - второе число 2) 23 + 1 = 24 - наибольшее из чисел ответ: 22; 23; 24.
Объяснение:
1)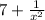
2)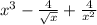
3) 15x⁴ + 2
4) 8x - 3
Элементарно же!