Большое количество задач такого типа решаются при формулы Ньютона-Лейбница:
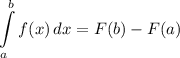
Поэтому, во-первых, нужно найти 
и 
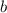- абсциссы точек пересечения графиков функций. Для этого нужно решить несложное уравнение:
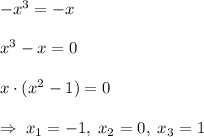
А так как есть целых три точки пересечения, то придется считать два интеграла: первый - от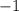 
до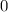 
(как результат приравнивания функций: 
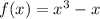), а второй - от 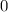до 
(здесь уже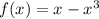 
):
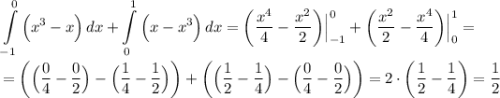
Значит, площадь искомой фигуры (состоящей из нескольких других фигур) равна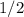 
или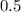 
(каких-то квадратных единиц измерения), если перевести в десятичную дробь.
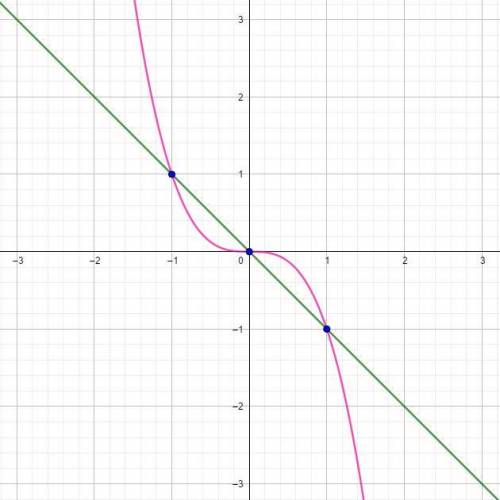
Большое количество задач такого типа решаются при формулы Ньютона-Лейбница:
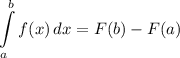
Поэтому, во-первых, нужно найти и 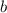- абсциссы точек пересечения графиков функций. Для этого нужно решить несложное уравнение:
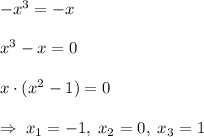
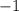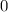А так как есть целых три точки пересечения, то придется считать два интеграла: первый - от до (как результат приравнивания функций: 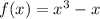), а второй - от 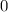до (здесь уже ):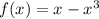
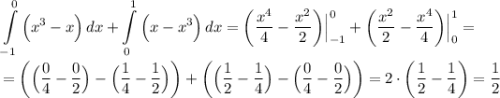
Значит, площадь искомой фигуры (состоящей из нескольких других фигур) равна 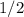или 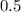(каких-то квадратных единиц измерения), если перевести в десятичную дробь.
Начальные преобразования (общие для обоих методов).{2x+3y=34x2−9y2=27⇒{2x+3y=38x−18y=27Решение методом подстановки.{2x+3y=38x−18y=27⇒{y=−23x+18x−18y=27⇒{y=−23x+18x−18(−23x+1)=27⇒{y=−23x+120x−45=0⇒{y=−23x+1x=94⇒{y=−0,5x=94ответ:(94;−12)=(214;−12)≈(2,25;−0,5)Решение методом сложения.{2x+3y=38x−18y=27Складываем уравнения:+{2x+3y=38x−18y=27∣⋅66(2x+3y)+(8x−18y)=6⋅3+2720x=45x=94Подставиим найденную переменную в первое уравнение:2(94)+3y=3y=−0,5ответ:(94;−12)=(214;−12)≈(2,25;−0,5)