1. Сумма углов n-угольника равна 180°(n-2).
В случае 12-угольника сумма равна 1800 градусов. Т. к. он правильный, то углы его равны 1800/12=150 градусов. ответ : 150°
2. Площадь параллелограмма равна произведению его основания (a) на высоту (h):
S = a ⋅ h
144 см² = а ⋅ 16 см
a = 9 см
3.s = a * b / 2
a - катет b - катет
a = 12
b^2 = 13^2 - 12^2
b^2 = 169 - 144
b^2 = 25
b = 5
S = 5 * 12 / 2
S = 30
4. Площадь ромба можно найти по формуле S = 0,5d₁d₂, где d₁ и d₂ - его диагонали.
Т.к. ромб - это параллелограмм, у которого все стороны равны, то он обладает всеми свойствами параллелограмма, а именно: диагонали ромба точкой пересечения делятся пополам. Значит, полусумма диагоналей равна 28 : 2 = 14 (см).
Свойство ромба: диагонали ромба перпендикулярны. Значит, при пересечении диагоналей ромба получаются 4 прямоугольных треугольника, у которых катеты - половины диагоналей, а гипотенуза - сторона ромба.
Рассмотрим один из прямоугольных треугольников и, применив теорему Пифагора, найдем его катеты.
Пусть один из катетов х см, тогда второй будет равен (14 - х) см. Т.к. сторона ромба равна 10 см, то составим и решим уравнение:
х² + (14 - х)² = 10²,
х² + 196 - 28х + х² - 100 = 0,
2х² - 28х + 96 = 0,
х² - 14х + 48 = 0.
D = (-14)² - 4 · 1 · 48 = 196 - 192 = 4; √4 = 2
х₁ = (14 + 2)/(2 · 1) = 16/2 = 8, х₂ = (14 - 2)/(2 · 1) = 12/2 = 6
Если один из катетов равен 8 см, то второй будет равен 14 - 8 = 6 (см). Тогда диагонали ромба будут равны 16 см и 12 см, а площадь
S = 0,5 · 16 · 12 = 96 (см²)
Если один из катетов равен 6 см, то второй будет равен 14 - 6 = 8 (см). Тогда диагонали ромба будут равны 12 см и 16 см, а площадь
S = 0,5 · 12 · 16 = 96 (см²)
ответ: 96 см².
5.Обозначим трапецию АВСД. угол С=угол Д=90 градусов. так как в трапецию можно вписать окружность, то суммы противоположных сторон равны ВС+АД=СД+АВ.
проведём высоту ВК. Она разделила трапецию на прямоугольник ДСВК и прямоугольный треугольник АВК. Так как острый уголА = 45 градусов, то второй острый угол АВК = 90-45=45 градусов, значит треугольник равнобедренный, ВК=АК.
Пусть АК=х тогда и ВК=х, по т. Пифагора х²+х²=(12√2)², 2х²=144·2, х²=144, х=12, АК=12 см, ВК=12 см, тогда и СД=12 см.S(ABCD)=1/2·(АД+ВС)·ВК=1/2·(12+12√2)·12=72·(1+√2)
Объяснение:
Часть 1
1. Параллелограммом называется четырехугольник, у которого противолежащие стороны ...
1.параллельны
2.равны
3.пересекаются
4.перпендикулярны
2. Дайте название следующему утверждению: в параллелограмме противоположные стороны равны. 1.определение параллелограмма
2.признак параллелограмма
3.аксиома
4.свойство параллелограмма
3)В параллелограмме ABCD углу А противоположным будет угол ?
1. В
2. С
3. D
4. В параллелограмме нет противоположных углов
4. Какова сумма любых двух соседних углов в параллелограмме?
1) 180°
2) бывает разной
3) 270°
4) 90°
5. В четырехугольнике два противоположных угла равны. Является ли он параллелограммом?
1) не является
2) не обязательно
3) такая ситуация невозможна
4) является
6. Один из углов параллелограмма равен 35°. Чему равны остальные его углы?
1) 145°, 35°, 145°;
2) 55°, 125°, 5°;
3) 35°, 145°, 50.
Сумма двух соседних углов равна 180°, значит второй угол : 180 - 35= 145°. Противоположные углы в параллелограмме равны , значит оставшиеся углы : 145°;35°; 145°
7. Биссектрисы соседних углов параллелограмма:
1) перпендикулярны
2) параллельны
3) пересекаются и точкой пересечения делятся пополам
4) невозможно их провести
8. Продолжите: Биссектриса угла в параллелограмме отсекает от него равнобедренный треугольник.
9. Вставьте пропущенное слово: В параллелограмме противоположные стороны равны
10.Вставьте пропущенные слова: Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник параллелограмм
Часть 2 (задачи)
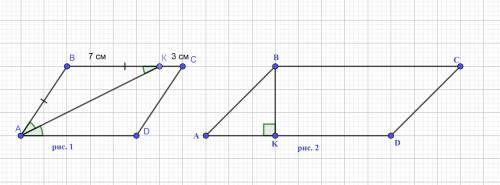
1.В параллелограмме АВСD биссектриса угла А пересекает сторону ВС в точке К так, что ВК = 7 см, КС = 3 см. Чему равен периметр параллелограмма?
Биссектриса угла в параллелограмме отсекает от него
равнобедренный треугольник, поэтому Δ АВК равнобедренный, значит АВ=ВК= 7 см
Сторона ВС=ВК+ КС= 7+3=10 см
Р=2*(АВ+ВС) =2*(10+7)=2*17 =34 см
ответ : Р= 34 см
( рис. 1 во вложении)
2. Из вершины В параллелограмма ABCD с острым углом А проведен перпендикуляр BK к прямой AD; ВК =1/2АВ. Найдите углы С и D
Рассмотрим Δ ABK. ( рис. 2) Он прямоугольный (∠ ВКА = 90°).
По условию BK = 1/ AB. А поскольку AB – гипотенуза Δ АВК ., то ∠ А = 30 ° (катет, лежащий против угла в 30 ° равен половине гипотенузы).
Поскольку в параллелограмме противолежащие углы равны, то
∠ С = 30 °
Теперь найдем ∠ D. В параллелограмме сумма внутренних углов равна 360 ° , значит
∠ D = ∠B = (360° - 2*30°):2= 150°.
ответ: C = 30 градусов, D = 150 градусов
( рис.2 во вложении)
Объяснение: 1) Упростим выражение.
2а³+9 -2 (а+1)(а²-а+1)=
=2а³+9- 2(а³+1³)= 2а³+9-2а³-2=7
Проверим на полном выражении: при а=0,5
2*(0,5)³+9-2(0,5+1) (0,5²-0,5+1)=2*0,125+9 - 2*1,5*(0,25+0,5)=
= 0,25+9-3*0,75= 9,25-2,25=7
2)Упростим выражение:
х(х+2)(х-2) -(х-3)(х²+3х+9)=
=х(х²-4) - (х³-27) =х³-4х-х³+27= -4х+27
при х=1/4
-4*(1/4) +9=-1+27=26
Проверим на полном выражении: при х =1/4=0,25
0,25(0,25+2)(0,25-2)- (0,25-3)(0,25²+3*0,25+9)=
=0,25*2,25*(-1,75) - (- 2,75 ) *(0,0625+0,75+9)=
= -0,984375 - (-2,75)* 9,8125= 26,984375- 0,984375=
=26
3) 3(b-1)²+(b+2)(b²+2b+4) - (b+1)²=
= 3(b²-2b+1)+(b+2)( b²+2b+2²)-(b²+2b+1)=
= 3b²-6b+3+b³+2b²+4b+2b²+4b+8-b²-2b-1=
=(3b²+2b²+2b²-b²)+(-6b+4b+4b-2b)+(3+8-1)+b³=
= 6b²+10+b³= b²( 6+b)+10
Может можно как-то проще сократить...
b=-1/3
(-1/3)² (6+1/3)+10= 1/9 * 6 1/3 +10 = 19/27 + 10=10 19/27
4) в выражении знак пропущен...