Question

Докажите, что кроме р1, существуют и другие простые числа. ( : ( я даже не знаю с чего начать)

Answer 1

Пусть простых чисел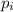 $p_i$ всего M.  Рассмотрим число 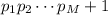$p_1p_2\cdots p_M+1$. Оно не делится ни на одно из чисел 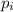$p_i$, поэтому оно простое. Но по предположению все простые числа меньше этого числа, поэтому оно должно быть составным. Противоречие.

Обычно в доказательствах опускается вставка, что число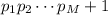 $p_1p_2\cdots p_M+1$ не совпадает ни с одним из чисел 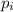$p_i$. Несмотря на то, что это очевидно, мне кажется, что для строгости доказательства об этом забывать нельзя.

Answer 2

Предположим что это не так. То есть p1 p2 pm конечное чило простых чисел.

Выпишем все простые числа

p1 p2 p3 pm

Составим число a = p1+P2+p3+p4+p5 +pm+1

чило а имеет хотя бы один простой делитель т.е. число а делится на одно из чисел p1 p2 p3 pm НО 1 не делиться не делиться не на одно из этих чисел  отсюда а не делиться не на одно из этих чисел

Получили противоречение. ПОэтому делаем вывод ПРОСТЫХ ЧИСЕЛ БЕСКОНЕЧНО МНОГО