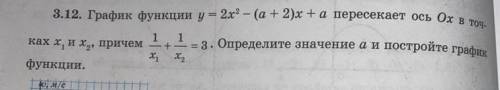
1.
√3 + tg15° = √3 + tg(45°-30°) = √3 + tg45° - tg30°/1 + tg45°×tg30° = √3 + 1 - √3/3 / 1 + 1×√3/3 = √3 + 1 - √3/3 / 1 + √3/3 = √3 + 3-√3/3 / 3+√3/3 = √3 + 3-√3/3+√3 = √3 + (3 - √3)×(3 - √3)/6 = √3 + (3 - √3)²/6 = √3 + 9 - 6√3 + 3/6 = √3 + 12-6√3/6 = √3 + 6(2-√3)/6 = √3+2-√3 = 2
ответ: d) 2
2.
8sin15° × cos15° + √3 × tg60° = 4sin30° + √3 × √3 = 4×1/2 + (√3)² = 2+3 = 5
ответ: c) 5
3.
а) tg225° + sin30° = tg(180°+45°) + 1/2 = tg45° + 1/2 = 1 + 1/2 = 3/2 = 1,5
б) √2 × cos315° = √2 × cos(360°-45°) = √2 × cos(-45°) = √2 × cos45° = √2 × √2/2 = (√2)²/2 = 2/2 = 1
ответ: а) 1,5 б) 1
Объяснение:
ответ: a=1.
Вершина параболы:
y'=(2x^2-3x+1)'=4x-3=0
4x=3 |:4
x=0,75. ⇒
y=2*0,75²-3*0,75+1=2*0,5625-2,25+1=1,125-2,25+1=-0,125. ⇒
(0,75;-0,125).
Пересечение графика с осью ОХ:
2x²-3x+1=0
2x^2-2x-x+1=0
2x*(x-1)-(x-1)=0
(x-1)*(2x-1)=0
x₁=1 x₂=0,5. ⇒
(0,5;0) (1;0).
x=0 y=2*0^2-3*0+1=1 ⇒ (0;1)
x=1,5 y=2*1,5^2-3*1,5+1=2*2,25-4,5+1=4,5-4,5+1=1. ⇒ (0;1).