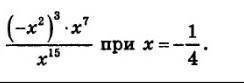
Площадь прямоугольника равна половине произведения квадрата диагонали на синус угла между ними
S=1\2d^2 *sin альфа
(альфа - острый угол между диагоналями
бэта - тупой угол между диагоналями,
углы альфа и бэта смежные)
откуда
sin альфа=2S\d^2
sin альфа=2*12\ (5*5)=24\25
cos альфа=корень(1-sin^2 альфа)=корень(1-(24\25)^2)=7\25
cos бєта=сos (180-альфа)=-cos альфа=-7\25
по теореме косинусов
(учитывая равенство диагоналей, и деление их в точке пересечния пополам)
стороны прямоугольника равны
a=корень(2.5^2+2.5^2-2*2.5*2.5*7\25)=корень(2*2.5^2*(1-7\25))=
=2.5\5*корень(2*(25-7))=0.5*6=3
b=корень(2.5^2+2.5^2+2*2.5*2.5*7\25)=корень(2*2.5^2*(1+7\25))=2.5\2*корень(2*(25+7))=0.5*8=4
(3*4=12
3^2+4^2=5^2)
периметр прямоугольника равен P=2(a+b)=2*(3+4)=14
ответ: 14 см
1) Согласно соотношению между средним арифметическим и средним геометрическим 1 + а₁ ≥ 2 * √а₁ ; 1 + а₂ ≥ 2 * √а₂ ; ... ; 1 + аn ≥ 2 * √аn
Перемножив все эти соотношения, получаем
(1+а1)*(1+а2)*...* (1+an) ≥ 2 * √а₁ * 2 * √а₂ *...* 2 * √аn =
2^n * √ (а₁ * а₂ *...*an) = 2^n
2) Поскольку медианы точкой пересечения делятся в отношении 2 : 1, считая от вершины, то отношение расстояния от данной точки до вершины треугольника к длине медианы равно 2 : 3 и соответственно длина данного отрезка равна 2/3 стороны треугольника, то есть 4 см.
(-х^2)^3 · x^7 / x^15 = -x^6 · x^7 / x^15 = -x^13/x^15; при х = -1/4 = 1/4^13 / 1/4^15 = 0.25^13 / 0.25^15 = 1 / 0.25^2 = 0.0625