В решении.
Объяснение:
Решить графически систему уравнений:
у = х² - 7
у = |x|
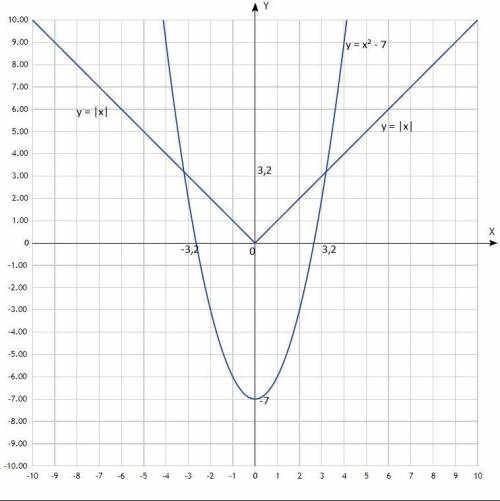
Первый график - парабола со смещённым центром, ветви направлены вверх.
Второй график - график функции модуля (значения у всегда > 0).
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = х² - 7 у = |x|
Таблицы:
х -4 -3 -2 -1 0 1 2 3 4 х -3 -2 -1 0 1 2 3
у 9 2 -3 -6 -7 -6 -3 2 9 у 3 2 1 0 1 2 3
По вычисленным точкам построить графики.
Согласно графиков, координаты точек пересечения:
(-3,2; 3,2); (3,2; 3,2).
Решения системы уравнений: (-3,2; 3,2); (3,2; 3,2).
В решении.
Объяснение:
Решить графически систему уравнений:
у = х² - 7
у = |x|
Первый график - парабола со смещённым центром, ветви направлены вверх.
Второй график - график функции модуля (значения у всегда > 0).
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = х² - 7 у = |x|
Таблицы:
х -4 -3 -2 -1 0 1 2 3 4 х -3 -2 -1 0 1 2 3
у 9 2 -3 -6 -7 -6 -3 2 9 у 3 2 1 0 1 2 3
По вычисленным точкам построить графики.
Согласно графиков, координаты точек пересечения:
(-3,2; 3,2); (3,2; 3,2).
Решения системы уравнений: (-3,2; 3,2); (3,2; 3,2).

Если нарисовать график, то всё на нём будет видно.
у=х²+6х+8 - это парабола с ветвями, направленными вверх, точки пересечения с осью ОХ - х₁= -4, х₂= -2 (это корни уравнения х²+6х+8=0)
Вершина находиться в точке х(верш)= -в/2а=-6/2=-3, у(верш)=(-3)²+6*(-3)+8= -1.
График ф-ции у=|x²+6x+8| получаем из предыдущего путём отображения относительно оси ОХ той части параболы, которая лежит ниже оси ОХ( на отрезке [-4,-2] ) в верхнюю полуплоскость.
Чтобы прямая у=а (параллельная оси ОХ) пересекла этот график в 4 точках, надо, чтобы это число а было между 0 и 1, то есть 0<а<1