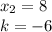
Объяснение:
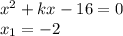
По теореме Виета:
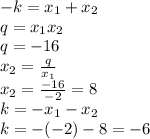
1) -3х+6у-12х-9у= -15x-3y
2) 6mn-2m-11mn-3n-5m=-5mn-7m-3n
1) (3a-7b)-(4a+8b)= 3a-7b-4a-8b=-a-15b
2)-(5m-7n)+(2n+12m)=-5m+7n+2n+12m=7m+9n
3) 3x(1-4x)-5x(6x+7) =3x-12x-30x-35x=-74x
4) 5c(2c+a)+(3c-2a)(5a-2c)=10c^2+5ca+15ca+6c^2-10a^2+4ca=16c^2+24ca-10a^2
5) (5y-3) куб. -(2-5y)куб=125y^3-225y^2+45y-27-8+150y - 60y^2+125y^3 =250y^3-285y^2+195y-32
1) 13(а-2)+10(4-а)=23
13a-26+40-10a=23
3a=9
a=3
2) (2х-1)(х+1)-х куб.=(х-3)куб -10
2x^2+2x-x-1-x^3=x^3-6x^2+27x-10
8x^2-28x-2x^3=-9
x(8x-28-2x^2)=-9
x1=0 (8x-28-2x^2)=-9
-2x^2+8x-19=0
D=8^2-4*(-2)-(-19)=-88(нет корней)
ответ:0
3) x/4 + x/8 =3/2
3x/8=3/2
3x=8*3/2
3x=12
x=4
Повторные независимые испытания. Схема Бернулли. Число попаданий - случайная величина, принимающая значения от 0 до 5. Найдем вероятности появления этих значений.
Вероятность Значения 0. Число сочетаний из 5(выстрелов всего) по 0(рассматриваемое значение) - это 1 - умножим на 0.5 в степени 0 и на 1-0.5 в степени 5-0. Получаем 0.03125. Это 1/32.
Вероятность значения 1. Число сочетаний из 5 по 1 - это 5 - умножается на 0.5 в степени 1 и на 1-0.5 в степени 5-1. Получаем 0.15625. Это 5/32.
Вероятность значения 2. Число сочетаний из 5 по 2 - это 10 - умножаем на 0.5 в степени 2 ина 1-0.5 в степени 5-2. Получаем 0.3125. Это 10/32.
Далее вероятности располагаются в обратном порядке в силу симметричности числа сочетаний и того, что 1-0.5 равно 0.5.
Ряд распределения:
0 1 2 3 4 5
0,3125 0,15625 0,3125 0,3125 0,15625 0,03125
Проверка. Сумма всех вероятностей равна 1.
-6
Объяснение:
(-2)^2+k(-2)-16=0
4-2k-16=0
-2k=16-4
-2k=12
k=-6