3) с2 – d2 = (с – d)(c + d); 4) 92 – а2 = (9 – а)2?
695. Розкладіть на множники:
1) х2 – 49; 2) 100 - p2;
3) 0,04m2 - n2;
4) 25х2 – 36уг; 5) 16а2 – b2c2; 6) 121m2a2
1
-b2.

Question

Алгебра: 3) с2 – d2 = (с – d)(c + d); 4) 92 – а2 = (9 – а)2? 695. Розкладіть на множники: 1) х2 – 49; 2) 100 - p2; 3) 0,04m2 - n2; 4) 25х2 – 36уг; 5) 16а2 – b2c2; 6) 121m2a2 1 -b2.

agnesaudal · Accepted Answer

Надо взять такие числа, которые будут максимально равны между собой и при этом будут являться целыми.

Эти числа 9 и 9.

Проверим по квадратам:

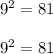
$9^{2}=81\\\\ 9^{2}=81\\\\$

81 + 81 = 162

Теперь проверим другие числа. Один множитель уменьшим на единицу, а другой увеличим на единицу:

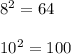
$8^{2}=64\\\\ 10^{2}=100$

64 + 100 = 164

Как видим сумма получилась больше предыдущей. Возьмём еще:

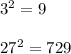
$3^{2}=9\\\\ 27^{2}=729$

9 + 729 = 738

Значительно больше первой суммы. Вывод:

надо уравнять множители, чтобы получить наименьшую сумму квадратов этих множителей.

ответ: 81 = 9 * 9, т.к. 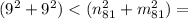$(9^{2}+9^{2})<(n_{81}^{2}+m_{81}^{2})=$

162 < суммы квадратов множителей (при "n" </> 9, "m" </> 9).

*n81^2 - квадрат множителя 81.

3) с2 – d2 = (с – d)(c + d); 4) 92 – а2 = (9 – а)2? 695. Розкладіть на множники: 1) х2 – 49; 2) 100 - p2; 3) 0,04m2 - n2; 4) 25х2 – 36уг; 5) 16а2 – b2c2; 6) 121m2a2 1 -b2.

MOGZ ответил

3) с2 – d2 = (с – d)(c + d); 4) 92 – а2 = (9 – а)2?
695. Розкладіть на множники:
1) х2 – 49; 2) 100 - p2;
3) 0,04m2 - n2;
4) 25х2 – 36уг; 5) 16а2 – b2c2; 6) 121m2a2
1
-b2.