Ну сначала надо это изобразить эту красоту. Очевидно, что шар описан около тетраэда.
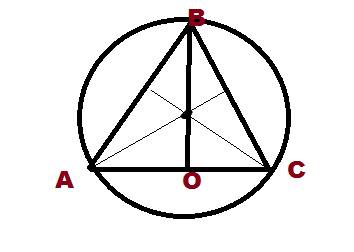
Второй чертеж - наша красота в сечении. То есть рассекаем через центр и вершину тетраэда. Получаем в сечении правильный треугольник, который вписан в круг. (я сделала его во вложении). Если мы построим медианы/высоты/биссекрисы, то они пересекуться в центре круга. По своействам правильного треугольника, его медианы/высоты/биссектрисы делятся точкой пересечения 2к1 от вершины то есть наш радиус это 2/3 от высоты треугольника. Находим высоту. (3√2*3)/2=4,5√2.
Теперь рассмотрим половину нашего треугольника, которую мы отделили высотой (то есть треугольник ОСВ. Угол С=60°, така как правильный треугольник.
sinC=BO/BC=√3/2
BO=4,5√2. BC - искомая сторона
4,5√2/BC=√3/2
4,5√2=√3/2 *ВС
9√2/√3 = ВС
2) Четность-нечетность:
Т.к.
3) Точки пересечения с Ox. Решим исходное уравнение при y = 0. (метод решения: Виета-Кардано)
Получим один корень: x = 0.148 - абсцисса точки пересечения графка с осью Ox. Координаты точки: (0.148; 0)
Точка пересечения с Oy. Найдем y, подставив в уравнение x = 0. Получим: y = -5. Координаты точки: (0, -5).
4) Так как функция кубическая, то точек экстремума не имеет.
5) Первая производная.
2. Вторая производная.
Находим корни уравнения. Для этого полученную функцию приравняем к нулю.
Откуда точка перегиба:
x = 5/3
На промежутке: (-∞ ;5/3)
Значит, функция выпукла.
На промежутке (5/3; ∞)
Значит, функция вогнута.
6)
7(график в приложениях)
Как мог.. Работа объемная, конечно)