Сторона данного треугольника а(3) равна Р:3=6√3:3=2√3 дм
Формула радиуса окружности, описанной около правильного треугольника:
R=a/√3 =>
R=2√3:√3=2 дм
Формула стороны правильного многоугольника через радиус вписанной окружности:
а(n)=2r•tg(180°:n), где r – радиус вписанной окружности, n – число сторон,
Для правильного шестиугольника tg(180°:n)=tg30°=1/√3
a₆=2•2•1/√3=4/√3
P=6•4/√3=8√3 дм
—————
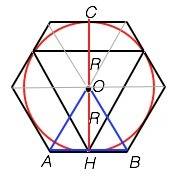
Как вариант: Правильный шестиугольник состоит из 6 равных правильных треугольников.
На рисунке приложения ОН - радиус описанной около правильного треугольника окружности и в то же время высота одного из 6 правильных треугольников, все углы которого 60°; АВ - сторона шестиугольника. Задача решается с т.Пифагора.
2.прямая.
3.равны и не параллельны
4.функция вида
5.формулой вида у=kх, где х-независимая переменная, к- не равное нулю.
6.множество, на котором задается функция. в каждой точке этого множества значение функции должно быть определено . ОДЗ
7. число, стоящее посередине упорядоченного по возростанию ряда чисел. если кол-во чисел в ряду чётное, то медианой ряда является полусумма двух стоящих посередине чисел.
8.число, которое встречается в данном ряду чаще других
9. разность между наибольшим и наименьшим из этих чисел.
10.от одной переменной можно привести к виду. кол-во решений зависит от параметров а и b.
11.найти множество всех его решений или доказать, что корней нет.
12.тождество
13. чтобы к сумме двух чисел прибавить третье число можно к первому числу прибавить сумму второго и третьего числа. а+b+c
14. верными и неверными