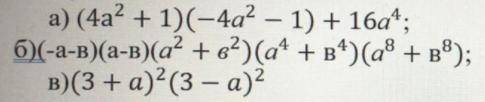
Задача №2. Пусть Х - скорость течения реки, тогда скорость катера по течению равна (8+Х) км/ч, а против течения (8-Х) км/ч. Тогда на путь по течению он затратил 15/(8+Х) ч, а на путь против течения 15/(8-Х) ч.
Т. к. по условию на весь путь туда и обртно затрачено 4 ч, составим уравнение:
15/(8+Х) + 15/(8-Х) = 4 (приводим к общему знаменателю (8+Х) *(8-Х) = 8^2 - Х^2 = 64 - Х^2 )
(120 + 15Х + 120 - 15Х - 4(64 +Х^2) ) /64 - Х^2 = 0
система:
120 + 15Х + 120 - 15Х - 4(64 +Х^2) = 0
64 - Х^2 не равоно 0
Решаем первое ур-ние системы:
240 -256 + 4Х^2 = 0
4Х^2 = 16
Х^2 = 4
Х = 2
x+x+x-3=51
3x-3=51
3x=54
x=18
боковые по 18, а основание равно 18-3=15
1 вариант
х - одна сторона треугольника, т.к. треугольник равнобедренный, то 2-я сторона - тоже х , а 3-я сторона - х-3, т.к. сумма всех сторон = 51 см, составим ур-е
х+х+х-3=51
3х-3=51
3х=54
х=18 см - боковые стороны
51-(18*2) = 15 см , или 18-3 = 15 см - основание
Проверка: 18+18+15=51 см
2 вариант:
(х-3) - боковые стороны
х - основание, тогда
2(х-3)+х=51
3х=57
х=19 см основание
19-3 = 16 см боковая сторона
Проверка:
16+16+19=51 см
а) (4а²+1)(-4а²-1)+16а⁴
(4а²+1)(-(4а²+1)+16а⁴
-(4а²+1)(4а²+1)+16а⁴
-(4а²+1)²+16а⁴
-(16а⁴+8а²+1)+16а⁴
-16а⁴-8а²+1+16а⁴
-8а²+1
б)(-а-b)(a-b)(a²+b²)(a⁴+b⁴)(a⁸+b⁸)
(-b-a)(b-a)(b²+a²)(a⁴+b⁴)(a⁸+b⁸)
((-b)²-a²)(b²+a²)(a⁴-b⁴)(a⁸-b⁸)
(b²-a²)(b²+a²)(a⁴-b⁴)(a⁸+b⁸)
(b⁴-a⁴)(a⁴-b⁴)(a⁸-b⁸)
-(a⁴-b⁴)(a⁴-b⁴)(a⁸-b⁸)
-(a⁴-b⁴)²(a⁸-b⁸)
-(a⁸-2a⁴b⁴+b⁸)(a⁸-b⁸)
-(a¹⁶-a⁸b⁸-2a¹²b⁴+2a⁴b¹²+a⁸b⁸-b¹⁶)
-a¹⁶+2a¹²b⁴-2a⁴b¹²+b¹⁶
в) (3+а)²(3-а)²
((3+а)(3-а))²
(9-а²)²
81-18а²+а⁴
а⁴-18а²+81