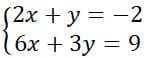
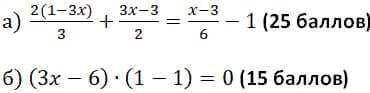
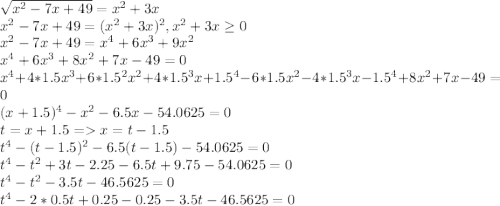
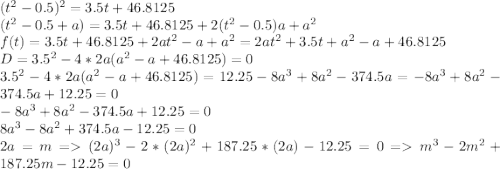
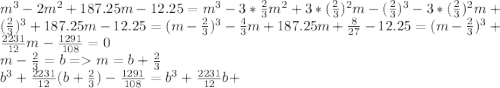
![\frac{2231}{18} - \frac{1291}{108} = b^3 +\frac{2231}{12}b + \frac{12095}{108} =0\\ Q = (\frac{q}{2})^2+(\frac{p}{3})^3 = (\frac{12095}{216})^2 + (\frac{2231}{36})^3 = \frac{12095^2+2231^3}{6^6} =\frac{11250781416}{6^6}\\ \sqrt{Q} = \frac{\sqrt{11250781416}}{216}\\b = \sqrt[3]{-\frac{q}{2}+\sqrt{Q}} + \sqrt[3]{-\frac{q}{2}-\sqrt{Q}}\\](/tpl/images/0683/3474/5b187.png)
![b = \sqrt[3]{-\frac{12095}{216}+\frac{\sqrt{11250781416}}{216}} + \sqrt[3]{-\frac{12095}{216}-\frac{\sqrt{11250781416}}{216}} = \frac{1}{6}*(\sqrt[3]{\sqrt{11250781416}-12095} - \sqrt[3]{\sqrt{11250781416}+12095})\\m = b +\frac{2}{3} = \frac{1}{6}*(\sqrt[3]{\sqrt{11250781416}-12095} - \sqrt[3]{\sqrt{11250781416}+12095} +4)\\m = 2a = a = \frac{m}{2} = \frac{1}{12}*(\sqrt[3]{\sqrt{11250781416}-12095} - \sqrt[3]{\sqrt{11250781416}+12095} +4)\\(t^2 - 0.5 + a)^2 = 3.5t + 46.8125 + 2(t^2-0.5)a + a^2\\](/tpl/images/0683/3474/6b782.png)
Да, кстати, корень кубического уравнения единственный в поле действительных чисел, так как его дискриминант больше нуля.
Теперь, при таком значении а правая часть вышенаписанного уравнения - это полный квадрат. Найдем корень, учитывая это:
![t_0 = \frac{-b}{2a} = \frac{-3.5}{4a} = -\frac{7}{8a} = -\frac{7}{8*\frac{1}{12}*(\sqrt[3]{\sqrt{11250781416}-12095} - \sqrt[3]{\sqrt{11250781416}+12095} +4)} = \frac{21}{2(\sqrt[3]{\sqrt{11250781416}-12095} - \sqrt[3]{\sqrt{11250781416}+12095} +4)}\\](/tpl/images/0683/3474/7a199.png)
Теперь свернем правую часть в полный квадрат и решим обычное квадратное уравнение:
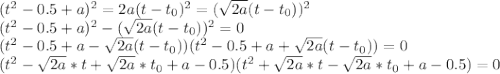
Рассмотрим первую скобку и найдем такие t, при которых она обнуляется. Получим:
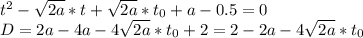
Честно говоря, мне кажется, в условии допущена ошибка. Циферки сами подставите и посчитаете, писать это неудобно.
Тартальи и Ферарро.
1) 0,36x^2 - 3,6x + 10 = (0,6x)^2 - 2*0,6x*3 + 3^2 - 3^2 + 10
Формула квадрата разности известна: (a-b)^2 = a^2 - 2ab + b^2
В нашем случае a = 0,6x; 3,6x = 2ab = 2*0,6x*b,
отсюда b = 3,6x/(2*0,6x) = 3,6/1,2 = 3.
Значит, нужно в конце прибавить 3^2 = 9, и тут же их отнять обратно.
Так получилась правая часть нашего равенства. Делаем дальше.
(0,6x)^2 - 2*0,6x*3 + 3^2 - 3^2 + 10 = (0,6x - 3)^2 - 9 + 10 = (0,6x - 3)^2 + 1
2) 8x^2 - 8√3*x + 12 = (2√2*x)^2 - 2*(2√2*x)*(√2*√3) + (√6)^2 - (√6)^2 + 12 =
= (2√2*x - √6)^2 - 6 + 12 = (2√2*x - √6)^2 + 6