1. Подставим координаты точек М и А в уравнение прямой. Затем выразим k. Если оба значения окажутся одинаковыми, то прямая проходит и через точку М и через точку А.
М (-3; -21)
-21=k(-3) ⇒ k=7
А (3; 21)
21=k3 ⇒ k=7
Вывод: прямая проходит через точки А и М. k=7.
2. у=6х+2
Коэффициент при х больше нуля, значит функция является возрастающей.
Значит на отрезке [0; 1] функция будет принимать наименьшее значение в точке 0.
у(0) = 6*0+2 = 2
ответ: на отрезке [0; 1] у наим. = 2
3. Чтобы найти координаты точки пересечения двух графиков, нужно решить систему уравнений, составленную из уравнений графиков.
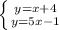
Первое уравнение умножим на 5.
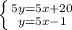
Из первого уравнения вычтем второе.
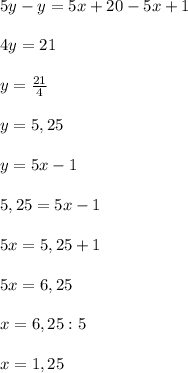
ответ: (1,25; 5,25)
1)
Раскрываем модуль и получаем два уравнения:
y₁=x²-6x+1-2x-1=x²-8x
y₁`=(x²-8x)`=2x-8=0
2x-8=0 |÷2
x-4=0
x=4 ⇒
y=|4²-6*4+1|-2*4-1=|16-24+1|-8-1=|-7|-9=7-9=-2. ⇒
(4;-2)
y₂=-(x²-6x+1)-2x-1=-x²+6x-1-2x-1=-x²+4x-2
y₂`=(-x²+4x-2)`=-2x+4=0
-2x+4=0 |÷(-2)
x-2=0
x=2 ⇒
y=|2²-6*2+1|-2*2-1=|4-12+1|-2*2-1=|-7|-4-1=7-5=2. ⇒
(2;2).
2)
√(2x²-8x+6)+√(4x-x²-3)<x-1
√(2*(x²-4x+3))+√(-(x²-4x+3))<x-1
Пусть x²-4x+3=t ⇒
√(2t)+√(-t)<x-1
ОДЗ:
x-1>0 x>1.
2t≥0 |÷2 t≥0
-t≥0 |×(-1) t≤0 ⇒ t=x²-4x+3=0
x²-4x+3=0 D=4 √D=2
x₁=3 x₂=1 ∉ОДЗ
ответ: x=3.