см, тогда второй катет - 
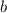см. Площадь прямоугольного треугольника равна 
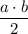, что составляет 210 см² или перепишем сразу 
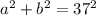
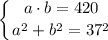
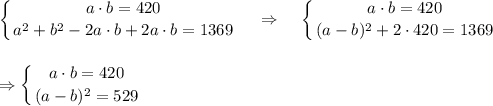
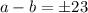. Тогда имеем несколько случаев.
, то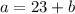 
и подставим в первое уравнение.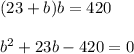
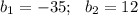см и корень 
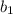не удовлетворяет заданному условию
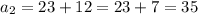см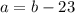
,то подставив в первое уравнение, получим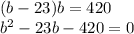
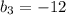
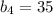см и корень 
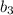не удовлетворяет условию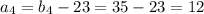
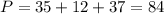см
ответ:
x∈(-∞; -6)∪(6; 10]
объяснение:
(x^2-16x+60)/(x^2-36)≤0
y=(x^2-16x+60)/(x^2-36)
(x^2-16x+60)/(x^2-36)=0
1) x^2-16x+60=0
d=256-4*60=256-240=16
2) x^2-36≠0
x^2≠36
x≠6
x≠-6
- + - +
---()()*>
(-6) (6) 10
x∈(-∞; -6)∪(6; 10]
1-56
2-47
3-59
Объяснение:
Я на 5 решил