243*(1/81) в степени 3х-2=27 в степени х+3
3 в пятой степени*(3 в минус четвертой степени) в степени 3х-2=(3 в 3) в степени х+3
3 в пятой степени*3 в степени -12х+8=3 в степени 3х+9
3 в степени 5-12х+8= 3 в степени 3х+9
5-12х+8=3х+9
5-12х+8-3х-9=0
-15х=-4
х=4/15
ответ: 4/15
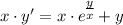
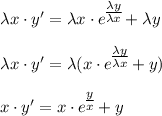
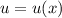 с замены:
с замены: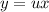 , тогда
, тогда 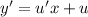
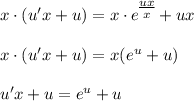
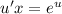
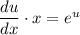 - уравнение с разделяющимися переменными.
- уравнение с разделяющимися переменными.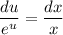 - уравнение с разделёнными переменными.
- уравнение с разделёнными переменными.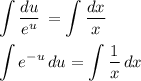
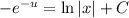 - общий интеграл новой функции.
- общий интеграл новой функции. из решения уравнения с разделяющимися переменными, чтобы записать решение исходного однородного уравнения, остаётся выполнить обратную замену:
из решения уравнения с разделяющимися переменными, чтобы записать решение исходного однородного уравнения, остаётся выполнить обратную замену: 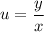
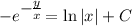 - общий интеграл исходного уравнения.
- общий интеграл исходного уравнения.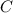 . Подставим в общий интеграл начальное условие:
. Подставим в общий интеграл начальное условие: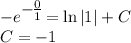
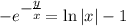 - частный интеграл, также является решением данного дифференциального уравнения.
- частный интеграл, также является решением данного дифференциального уравнения.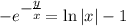
Представим все числа по основанию 3, т.е.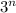
Возведем степень в степень, где это нужно
Т.к. основания равны, то и показатели будут равны, поэтому приравняем показатели
5+8-12x=3x+9
13-12x=3x+9
Перенесем с иксов в одну часть, без икса - в другую
13-9=3x+12x
4=15x
x=4/15
ответ: 4/15