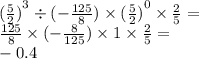
Условие
x ≥ –1, n – натуральное число. Докажите, что (1 + x)n ≥ 1 + nx.
Решение 1
Докажем неравенство индукцией по n.
База. При n = 1 неравенство превращается в равенство.
Шаг индукции. Пусть уже доказано, что (1 + x)n ≥ 1 + nx. Тогда (1 + x)n+1 ≥ (1 + nx)(1 + x) = 1 + nx + x + nx² ≥ 1 + (n + 1)x.
Решение 2
Пусть a > 1. Рассмотрим функцию f(x) = (1 + x)a – ax – 1, определенную при x > –1. Ее производная f'(x) = a(1 + x)a–1 – a = a((1 + x)a–1 – 1) положительна при x > 0 и отрицательна при –1 < x < 0. Следовательно, f(x) ≥ f(0) = 0 на всей области определения.
Замечания
1. Неравенство превращается в равенство не только при n = 1, но и при x = 0 . В остальных случаях оно строгое.
2. При x ≥ 0 (такое ограничение дано в источнике) неравенство Бернулли сразу следует из формулы бинома: (1 + x)n = 1 + nx + ... .
3. Из решения 2 видно, что неравенство верно и при нецелых n > 1.