Для начала найдем первообразную функции на всей числовой прямой:
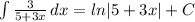
Знак модуля ставится ввиду того, что производная от модуля существует как в отрицательном значении, так и положительном, но так как задан промежуток интегрирования, на котором интегрируема функция получаем:
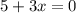
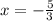
Получаем, что в данном промежутке произвадная существует только при положительном значении модуля, поэтому получаем:
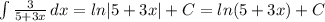
Что бы сравнить два числа a и b, нам дано равенство : b+2=a+√5 .
Глядя на него, мы можем понять, что если к числу b добавить 2, то оно будет равно числу а, которому добавили √5 .
Без решений и подбора чисел, можно узнать, что же больше, достаточно найти чему будет равен √5.
√5 = 2,24 .
Сравним числа, которые мы добавляем к нашим неизвестным 2 и 2,24 и увидим, что число 2 меньше.
Получается, что если мы к числу а добавим число большее, чем к числу b, то равенство выполняется.
Следовательно a < b.
task/29565495
Для функции у = f(x) найдите первообразную F(x), график которой проходит через точку M(a,b) и постройте график функции F (x) →
1. f(x) = 3x²-2 , M(2; 4) 2. f(x) = 3cosx - 2 , M(π/2, -1)
1. F(x) = ∫(3x² -2)dx =∫3x²dx - ∫2 dx = 3∫x²dx - 2∫dx =3*x³/3 -2x +C= x³ - 2x +C.
M(2; 4) ∈ F(x) ⇒ 2³ - 2*2 + C = 4 ⇒ C = 0 .
ответ : F(x) =x³ - 2x . * * * (x+√2)x(x -√2) * * *
2. F(x) = ∫(3cosx -2)dx =3∫cosxdx - 2∫dx = - 3sinx - 2x +C .
M(π/2, -1) ∈ F(x) ⇒ -1 = - 3sin(π/2) - 2*(π/2) + C ⇒ C = 2 - π .
ответ : F(x) = - 3sinx - 2x + 2 - π .
f(x)=3/(5+3x)
F(x)=F(3/(5+3x))=3F(1/(5+3x))=3*1/3 * ln|5+3x| + C = ln|5+3x|+C
Так как x = (-5/3;+беск), то |5+3x|=5+3x
=> F(x)=ln(5+3x)+C