Основная теорема алгебры. Уравнение n-го степеня имеет n корней. Иными словами: каков старший степень - столько и корней (действительные и комплексные)
Решим к примеру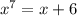 
уравнение в действительных корнях.
Рассмотрим функцию 
. Эта функция является возрастающей на всей числовой прямой.
Также рассмотрим правую часть уравнения: функцию 
. Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
графики пересекаются в одной точке, следовательно, уравнение имеет один действительный корень и 6 комплексно-сопряженные корни.
Возьмем теперь к примеру уравнение 
Если D>0, то квадратное уравнение имеет два ДЕЙСТВИТЕЛЬНЫХ корня.
Если D=0, то квадратное уравнение имеет два равные корни.
Если D<0, то квадратное уравнение действительных корня не имеет, но имеет два комплексно сопряженных корня.
1)
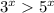
Так как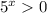 
при любых х, делим обе части неравенства на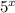 
⇒ 
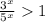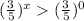
Показательная функция с основанием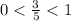 
убывает, то
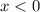
О т в е т.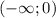 
2)
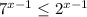
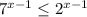
Так как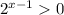 
при любых х, делим обе части неравенства на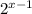 
⇒ 
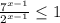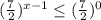
Показательная функция с основанием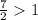 
возрастает, то
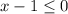
О т в е т. ![(-\infty;1]](/tpl/images/1361/5304/a162d.png)
3)
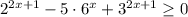
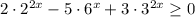
Так как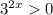 
при любых х, делим обе части неравенства на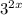 
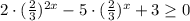
D=25-4·2·3=25-24=1
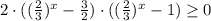
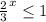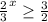
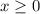или 
или 
О т в е т. ![(-\infty; -1]\cup [0;+\infty)](/tpl/images/1361/5304/edb57.png)
4)
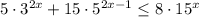
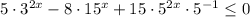
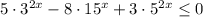
Так как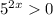 
при любых х, делим обе части неравенства на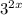
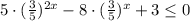
D=64-4·5·3=64-60=4
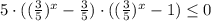
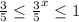
так как показательная функция с основанием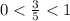 
убывающая, то
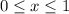
О т в е т. ![[0; 1]](/tpl/images/1361/5304/6a286.png)
cos^2x-5sinx*cosx+2=0
sinx=V1- cos^2x
cos^2x-5V1-cos^2x *cosx+2=0
cosx=t
t^2-5V1-t^2 * t+2=0
t^2+2=5V(1-t^2)*t
t^4+4t^2+4=25(1-t^2)t^2
t^4+4t^2+4=25t^2-25t^4
26t^4-21t^2+4=0
t=1/V2
t=2/V13
cosx=V2/2
x=pi/4+2pi*k
x=-pi/4+2pi*k
x=arccos(2/V13)+2pi*k
x=arccos(-2/V13)+2pi*k