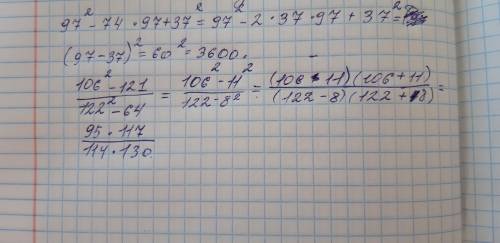
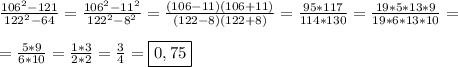
(106² - 121) / (122² - 64) = (106² - 11²) / (122² - 8²) = (106 - 11)(106 + 11) / (122 - 8)(122 + 8) = 95*117 / (114*130) =
разложим на простые множители
95 = 5*19
117 = 3*3*13
114 = 2*3*19
130 = 2*5*13
= 5*19 * 3*3*13 / (2*3*19 * 2*5*13) = 5 * 3*3 / (2*3 *2*5) = 3/4
Объяснение:
1) Положим, существует такое число, которое может выразиться несократимой дробью 
, при этом p - целое, q - натуральное, которое удовлетворяет соотношению:
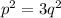
Из этого следует, что p², и p делятся на 3. Тогда p можно представить как 3c, тогда уравнение перепишется в виде:
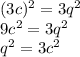
Отсюда следует, что и q делится на 3, а это противоречит условию несократимости дроби изначально. Следовательно на множестве рациональных чисел решений нет.
2) UPD: решается так же, немного не тот путь указал.
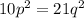
p² и p делятся на 21, значит p представимо в виде p = 21c
Тогда:
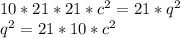
Стало быть, q тоже делится на 21, условие о несократимости дроби p/q нарушена, и значит решений нет на рациональном множестве
ответ:1. Вспомним формулы сокращенного умножения.
В нашем выражении присутствует вторая степень. Значит, можно воспользоваться формулами сокращенного умножения со второй степенью:
квадрат суммы: (a + b)^2 = a^2 + 2ab + b^2;
квадрат разности: (a - b)^2 = a^2 - 2ab + b^2;
разность квадратов: a^2 - b^2 = (a - b)*(a + b).
2. Выделим квадрат разности.
Проанализировав выражение, увидим, что 4а^2 - 20аb + 25b^2 похоже на квадрат разности. Определим значения для a и b.
4а^2 - 20аb + 25b^2 = (2a)^2 - 2*(2a)*(5b) + (5b)^2 = (2a - 5b)^2.
Подставим полученный квадрат разности в первоначальное выражение.
(2a - 5b)^2 - 36.
3. Разложим на множители.
Заметим, что 36 = 6^2. Подставим это в выражение.
(2a - 5b)^2 - 6^2.
Теперь мы имеем разность квадратов, где a = 2a - 5b, b = 6.
Подставим эти значения в формулу сокращенного умножения вместо a и b:
((2a - 5b) - 6)*((2a - 5b) + 6);
(2a - 5b - 6)*(2a - 5b + 6).
Следовательно, 4а^2 - 20аb + 25b^2 - 36 = (2a - 5b - 6)*(2a - 5b + 6).
Объяснение:
