ответ:пп3н3
Ппа
Объяснение:
Ппапккн3
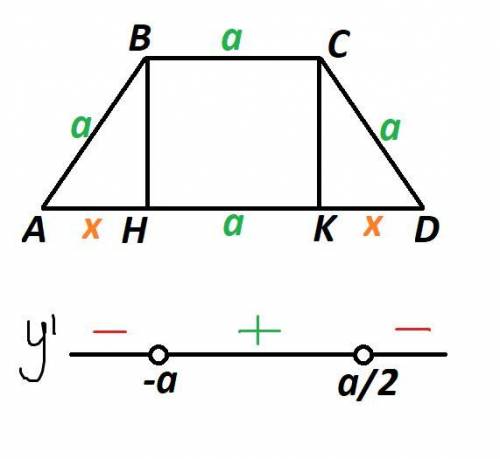
Рассмотрим трапецию ABCD.
Основания трапеции не могут иметь одинаковую длину, так как в противном случае это будет параллелограмм. Значит, одно из оснований BC и две боковые стороны AB и CD равны по а. Заметим, что рассматриваемая трапеция равнобедренная.
Проведем высоты BH и CK. Тогда, HK=а.
Обозначим AH=KD=х.
Высоту трапеции найдем по теореме Пифагора:
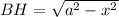
Запишем выражение для площади трапеции:
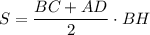
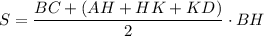
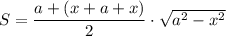
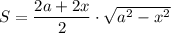
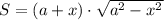
Исследуем на экстремумы функцию S. Найдем производную:
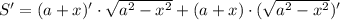
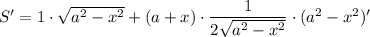
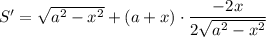
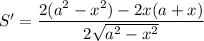
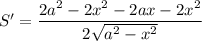
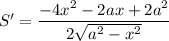
Найдем нули производной:
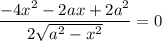
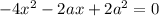
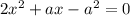
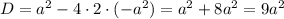
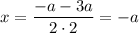
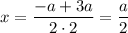
При переходе через точку 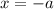 производная меняет знак с минуса на плюс, значит это точка минимума.
производная меняет знак с минуса на плюс, значит это точка минимума.
При переходе через точку 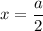 производная меняет знак с плюса на минус, значит это точка максимума.
производная меняет знак с плюса на минус, значит это точка максимума.
Таким образом, наибольшую площадь трапеция имеет при 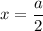 . Эта площадь равна:
. Эта площадь равна:
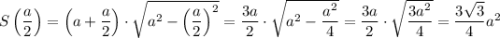
ответ: 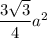
3. 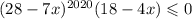
Заметим, что так как 2020 - четное число, то 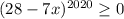 (число в четной степени всегда
(число в четной степени всегда 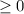 ). Поэтому первый множитель на знак левой части влиять не будет и его можно опустить. При этом стоит учесть, так это то, что если
). Поэтому первый множитель на знак левой части влиять не будет и его можно опустить. При этом стоит учесть, так это то, что если 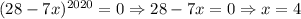 , то имеем :
, то имеем : 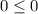 , а это верно. Поэтому нужно запомнить , что x = 4 - решение.
, а это верно. Поэтому нужно запомнить , что x = 4 - решение.
Если 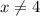 , то первый множитель положителен и на него можно поделить обе части, сохранив знак. Итого:
, то первый множитель положителен и на него можно поделить обе части, сохранив знак. Итого:
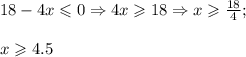
Решение неравенства - x = 4 и все 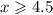 . Наименьшие целые решения - 4, 5 и 6. Их произведение равно 120.
. Наименьшие целые решения - 4, 5 и 6. Их произведение равно 120.
ОТВЕТ: 1) 120.
4. Область определения - все числа, которые можно подставить вместо x.
Под каждым из корней должно быть неотрицательное число, а знаменатель дроби должен быть отличен от 0. Область определения - все числа, удовлетворяющие системе из четырех неравенств 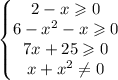 .
.
Из первого неравенства следует, что 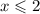 .
.
Решим второе неравенство: оно равносильно неравенству 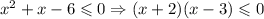 . Решением данного неравенство является отрезок [-2; 3].
. Решением данного неравенство является отрезок [-2; 3].
Третье неравенство: 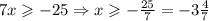 .
.
Четвертое: 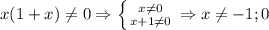
Так как у нас была система, ищем пересечение множеств решений всех 4 неравенств: ![x\in[-3;-1)\cup(-1;0)\cup(0;2].](/tpl/images/1359/4742/04668.png)
Все целые числа, принадлежащие области определения: -3; -2; 1; 2 (-1 и 0 выпадают, т.к. скобки круглые). Их сумма равна -2.
ОТВЕТ: 2) -2
3x + 2y = 8;
2x + 6y = 10,
применим метод подстановки. И начнем мы с того, что второе уравнение разделим на 2 и получим:
3x + 2y = 8;
x + 3y = 5.
Выражаем из второго уравнения переменную x:
x = 5 - 3y;
3x + 2y = 8.
Подставляем вместо x выражение из первого уравнения.
x = 5 - 3y;
3(5 - 3y) + 2y = 8.
Решаем первое уравнение системы:
3 * 5 - 3 * 3y + 2y = 8;
15 - 9y + 2y = 8;
-9y + 2y = 8 - 15;
-7y = -7;
y = 1.
Система уравнений:
x = 5 - 3 * 1 = 5 - 3 = 2;
y = 1.