1) 12 автомашин.
2) 15 автомашин
3) 5 тонн.
Объяснение:
Пусть х т перевозили на каждой машине фактически, тогда (х+1) т планировали перевозить.
Составляем уравнение и находим х:
60/х - 60/(х+1) = 3
60х + 60 - 60 х = 3х² + 3х
3х² + 3х - 60 = 0
х² + х - 20 = 0
х ₁,₂ = - 1/2 ± √((1/4) + 20) = -1/2 ± 9/2
х = 8/2 = 4 т - фактически перевозили на каждой автомашине;
х+1 = 5 т - планировали перевозить на каждой автомашине.
Теперь отвечаем на все вопросы.
1) Сколько автомашин требовалось сначала?
Сначала требовалось:
60 : 5 = 12 автомашин.
2) Сколько автомашин фактически использовали?
Фактически использовали:
60 : 4 = 15 автомашин
3) Сколько тонн груза планировалось перевозить на каждой машине?
На каждой автомашине планировалось перевозить 5 т груза.
я подозреваю что тут закралась неясность, в прогрессии насколько я помню количество элементов бесконечно, хотя в убывающей геометрической прогресии сумма всех элементов может сходиться.
инфми словами условие следует понимать так что n первых членов прогресии, где n = 2k,
выполняется условие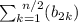 в три раза больше, чем
в три раза больше, чем 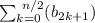
рассмотрим это более подробно на примере первых шести элементов
сумма нечетных S(1,3,5) = b1 + b3 + b5
сумма четных S(2,4,6) = b2 + b4 + b6 = b1*q + b3*q + b5*q = q(b1 + b3 + b5) = q*S(1,3,5)
следовательно отношение между четной суммой и нечетной равно знаменателю прогрессии.
Для нашей задачи это число 3
ответ 3