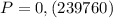Question

Из пруда, в котором плавают 15 щук, выловили 5 щук, пометили их и пустили обратно в пруд. во второй раз выловили 9 щук. какова вероятность того, что среди них окажутся две помеченные щуки?

Answer 1

$p=\frac{C_5^2\cdot C_{10}^7}{C_{15}^9}=\frac{\frac{5!}{2!3!}\cdot\frac{10!}{7!3!}}{\frac{15!}{9!6!}}=\frac{4\cdot5\cdot8\cdot9\cdot10\cdot6!}{2!3!\cdot10\cdot11\cdot12\cdot13\cdot14\cdot15}=\frac{4\cdot5\cdot8\cdot9\cdot10\cdot4\cdot5\cdot6}{2\cdot10\cdot11\cdot12\cdot13\cdot14\cdot15}= \\ =\frac{240}{1001}\approx0,24$

Answer 2

Возможность выбора "нужных" нам 2 щук из 5 определяется выражением

$C_5^2=\frac{5!}{(5-2)!2!}=\frac{5!}{3!2!}=\frac{5*4}{2}=10$

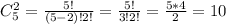
Возможность выбора "ненужных" нам 7 (так как 9-2=7) щук из 10 определяется выражением

$C_{10}^7=\frac{10!}{(10-7)!7!}=\frac{10*9*8}{3!}=10*3*4$

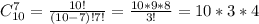
Всего щук 9 из 15. Возможность выбора 9 щук из 15 определяются выражением

$C_{15}^9=\frac{15!}{(15-9)!9!}=\frac{15!}{6!9!}=\frac{15*14*13*12*11*10}{6*5*4*3*2*1}$

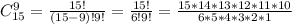
Вероятность 2-х щук из 9 будет равна соотношению произведения двух первых возможностей к последней возможности

$P=\frac{C_5^2*C^7_{10}}{C_{15}^9}=\frac{10*10*3*4*6*5*4*3*2*1}{15*14*13*12*11*10}=\frac{10*3*4*6*5*4*3*2*1}{15*14*13*12*11}=$

$\frac{10*6*5*4*3*2*1}{15*14*13*11}=\frac{10*6*5*4*3*2*1}{15*14*13*11}=\frac{10*6*4*2*1}{14*13*11}=\frac{10*6*4}{7*13*11}=0,(239760)$

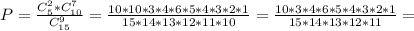
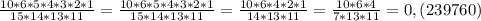
ответ:  $P=0,(239760)$