
sin20+sin40-cos10=0
Сложим синусы по формулам суммы:
2sin30*cos10-cos10=0
Вынесем общий множитель:
cos10(2sin30-1)=0
Произведение равно 0, когда хотя бы один из множителей равен 0, в данном случае
(2sin30-1)=(2*1/2-1)=0
2.sin3a-sina*cos2a
По формулам произведения умножим синус на косинус:
sin3a-1/2 (sin(-a)+sin3a)=sin3a+1/2 sina - 1/2 sin3a=1/2(sin3a+sina)
По формулам суммы сложим синусы:
1/2(sin3a+sina)=1/2*2sin2a*cosa=sin2a*cosa=2sina*cosa*cosa=2sina*cos^2 a
3.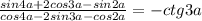
Т.к. в правой части ничего изменить нельзя, то будем работать только с левой части уравнения, пытаюсь представить ее в виде -ctg3a.
В числители вычтем синусы, в знаменателе - косинусы.
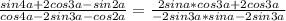
Вынесем в числителе и знаменателе общий множитель:
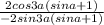
Сокращаем и получаем -cos3a/sin3a=-ctg3a
х(х-4)(х+4) =0
х1=0 х-4=0 отсюда х2= 4 х+4=0 отсюда х3= -4
рисуем луч, отмечаем эти точки
- 404⇒
Теперь возьми из интервала от минус ∞ до -4 любое значение и подставь его в данное первое неравенство вместо х, например х= -5
проверяем: (-5)³ - 16(-5)= -125+80= -45 <0 - верно, значит этот интервал подходит,
далее смотрим второй интервал, возьми точку
х= - 1, подставь в нерав-во (-1)³-16(-1)= -1 +16=15 <0 неверно!
второй интервал не подходит,далее,
третий интервал смотри от 0 до 4
возьми точку х=1 подставь её 1-16= -15< 0 -верно,
последний интервал от 4 до плюс+∞ Пусть х= 5
подставь 5³-16·5=125-80< 0 неверно
значит ответ такой :
Х⊂от - ∞до -4∪от 0 до 4, не включая точки -4,0,4 ,так как стоит строгий знак неравенства < ( без равно)
2) 4х³-х>0
х( 4х²-1)=0
х(2х-1)(2х+1)=0
Х1=0 2х-1=0 значитХ2= 1/2=0,5 2х+1=0 Х3= - 0,5
-0,500,5⇒ Точно также из четырех интервалов бери пробные точки и подставь в нерав-во 4х³-х>0
Интервалы, в которых пробные точки обратят неравенство в верное и будут объединенным решением , возьми пробные точки, например -1, -0,1 0,1; 1( это с первого по четвертый интервал)