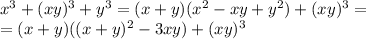
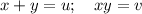 . Система примет вид
. Система примет вид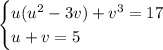
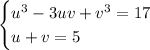
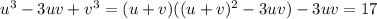
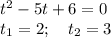
1.потому что корень это обратное действие возведению в квадрат! а любое число в квадрате положительное
2.В элементарной математике ноль не может быть основанием степени с отрицательным показателем, так как здесь существует правило не-деления на ноль.
В случае дробного отрицательного показателя степени ограничения на основание ужесточаются: основанием может являться только строго большее нуля число.
Для степеней с отрицательным показателем действительны все те же правила действий, что и для степени с натуральным показателем.
Объяснение:
пусть Х---скорость первого байкера
тогда Х-16---скорость второго байкера на первой половине пути
путь они проехали один и тот же S
время потратили одинаковое:
время первого байкера S/X
время второго байкера S/(2*(X-16)) + S/(2*120)
получим уравнение
S/X = S/(2*(X-16)) + S/(2*120)
1/X = 1/(2*(X-16)) + 1/(2*120)
2/X - 1/(X-16) = 1/120
(2*(X-16) - Х) / (Х*(X-16)) = 1/120
120*(X-32) = Х*(X-16)
120*X - 120*32 - Х*X + 16*Х = 0
Х*X - 136*X + 120*32= 0
D = 136*136 - 4*120*32 = 8*17*8*17 - 4*2*60*8*4 = 8*8*(17*17 - 60*4) = 8*8*(289-240) = 8*8*49
X1 = (136 + 8*7)/2 = 68 + 4*7 = 96
X2 = (136 - 8*7)/2 = 68 - 4*7 = 40---не удовлетворяет условию
ответ: скорость первого байкера 96 км/час
ПРОВЕРКА:
время в пути первого байкера S/96
время в пути второго байкера S/2 : (96-16) + S/2 : 120 = S/(2*80) + S/(2*120) = S/160 + S/240 = (3S+2S)/480 = 5S/480 = S/96
т.е. они доехали одновременно
x+y=t
xy=u
t+u=5 t=5-u
t^3+u^3-3ut=17 (5-u)^3+u^3-3u(5-u)=17
125-u^3-75u+15u^2+u^3+3u^2-15u-17=0
-90u+18u^2+108=0
u^2-5u+6=0 u=2 u=3
t=3 t=2
x+y=3 x+y=2
xy=2 xy=3 нет решения
x=1 y=2
x=2 y=1