Если первая труба наполняет бассейн за х часов, то вторая за (х+8) часов, в час первая труба наливает 1/х бассейна, вторая 1/(х+8) часть бассейна, за 3 часа вместе они наливают целый бассейн:
3*(1/х+1/(х+8)) = 1
общий знаменатель х*(х+8)
числитель будет: 3*(х+8+х)
дробь равна 1, значит числитель равен знаменателю
3*(2х+8) = х^2+8х
х^2+8x-6x-24 = 0
x^2+2x-24=0
D=4+96 = 100
x=(-2+-10)/2
x=-6 или х=4
Отриц. значение не подходит по смыслу задачи, значит х=4
в задаче спрашивалось про 2 трубу, она наполнит бассейн за 4+8 = 12 часов
Дана функция 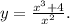
Производная её равна: y' = (3x^2*x^2 - 2x*(x^3 + 4))/x^4 = (x^3 - 8)/x^3.
Приравняем её нулю ( при х не равном 0 можно только числитель).
x^3 - 8 = 0.
x^3 = 8, х = ∛8 = 2. Это критическая точка.
С учётом разрыва функции при х = 0 имеем 3 промежутка монотонности функции: (-∞; 0), (0; 2) и (2; +∞).
На промежутках находим знаки производной.
Находится производная, приравнивается к 0, найденные точки выставляются на числовой прямой; к ним добавляются те точки, в которых производная не определена.
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = -1 0 1 2 3
y' = 9 - -7 0 0,7037.
• Минимум функции в точке: х = 2, у = 3.
• Максимума функции нет.
• Возрастает на промежутках: (-∞; 0) U (2; ∞).
• Убывает на промежутке: (0; 2).
Уравнение: Х+Х+2+2Х = 22
4Х +2 =22
4Х =22-2
4Х = 20
Х = 5; Х+2 = 7; 2Х = 10
ответ: 5см -одна сторона, 7см -другая сторона, 10см -3-ья сторона.
Задача №2.
Одна сторона = Хсм, другая сторона (Х+6)см, 3-ья сторона = (Х+9)см.
Уравнение:
Х + Х + 6 + Х + 9 = 33
3Х = 33 - 15
3Х = 18
Х = 6; Х+6 = 12; Х+9 = 15
ответ: 6см -одна сторона, 12см -другая сторона, 15 см -3-ья сторона.