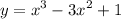
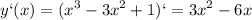
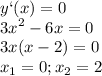
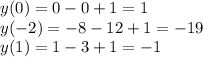
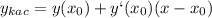
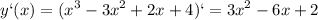
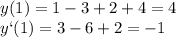
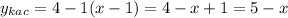
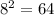 подходит
подходит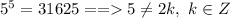 не подходит, так как непарная степень
не подходит, так как непарная степень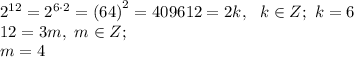
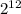 это будет квадрат 64
это будет квадрат 64 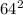 , и будет кубом от 16
, и будет кубом от 16 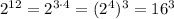 то-есть есть квадратом и кубон натуральніх чисел, поєтому не подходит
то-есть есть квадратом и кубон натуральніх чисел, поєтому не подходит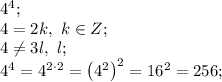 является квадратом натурального числа 16, и нету такого натурального числа, чтобы поднести в куб и получили данное
является квадратом натурального числа 16, и нету такого натурального числа, чтобы поднести в куб и получили данное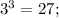 данное число уже является кубон натурального числа 3, а нутурального числа, чтобі в квадрате вышло 27 не существует
данное число уже является кубон натурального числа 3, а нутурального числа, чтобі в квадрате вышло 27 не существует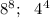
Поиск...
Избавься от ограничений
ПОПРОБУЙ ЗНАНИЯ ПЛЮС СЕГОДНЯ
Onyend
2 недели назад
Алгебра
5 - 9 классы
ответ дан • проверенный экспертом
1. Дана функция: у = х2 - 4х - 5
a) запишите координаты вершины параболы;
b) запишите ось симметрии параболы;
c) найдите точки пересечения графика с осями координат;
d) постройте график функции.
e) найдите промежутки убывания и возрастания функции;
2. Дана функция. у = -3х2 - 5х - 2.
а) Найдите значения функции f (2), f (−1) .
b) Известно, что график функции проходит через точку ( k ; 0). Найдите значение k.
3. Дана функция у = 2х2− 8x + 7.
Не строя графика, найдите:
а) область определения функции.
b) наименьшее значение функции.
1
СМОТРЕТЬ ОТВЕТ
Zombynella avatar
Ещё нужно решение?
romaahromov7 avatar
да решение очень нужно
oleg23goon avatar
на 1: определите, в каких четвертях находится график функции;
Zombynella avatar
График функции находится во ВСЕХ четырёх четвертях)
Войди чтобы добавить комментарий
ответ, проверенный экспертом
4,9/5
45
Zombynella
главный мозг
4.6 тыс. ответов
7.1 млн пользователей, получивших
В решении.
Объяснение:
1. Дана функция: у = х² - 4х - 5 ;
a) запишите координаты вершины параболы;
Формула: х₀ = -b/2a
x₀ = 4/2 = 2;
y₀ = 2² - 4*2 - 5 = 4 - 8 - 5 = -9.
Координаты вершины параболы (2; -9).
b) запишите ось симметрии параболы;
x = 2;
c) найдите точки пересечения графика с осями координат;
1) при пересечении графиком оси Оу х равен нулю:
у = х² - 4х - 5 ; х = 0
у = 0² -4*0 - 5 = -5;
Координаты пересечения графиком оси Оу (0; -5);
2) при пересечении графиком оси Ох у равен нулю:
у = х² - 4х - 5 ; у = 0
х² - 4х - 5 = 0, квадратное уравнение, ищем корни:
D=b²-4ac =16 + 20 = 36 √D= 6
х₁=(-b-√D)/2a
х₁=(4-6)/2
х₁= -2/2
х₁= -1;
х₂=(-b+√D)/2a
х₂=(4+6)/2
х₂=10/2
х₂=5.
Координаты пересечения параболой оси Ох (-1; 0); (5; 0).
d) постройте график функции.
График - парабола со смещённым центром, ветви направлены вверх.
Таблица
х -3 -2 -1 0 1 2 3 4 5 6 7
у 16 7 0 -5 -8 -9 -8 -5 0 7 16
График прилагается.
e) найдите промежутки убывания и возрастания функции;
Функция возрастает при х∈(2; +∞);
Функция убывает при х∈(-∞; 2).
2. Дана функция у = -3х² - 5х - 2.
а) Найдите значения функции f(2), f(−1).
Подставить в уравнение значение х и вычислить значение у:
1) у = -3х² - 5х - 2 х=2
у = -3 * 2² - 5*2 - 2 = -12 -10 - 2 = -24;
f(2) = -24.
2) у = -3х² - 5х - 2 х= -1
у = -3 * (-1)² - 5*(-1) - 2 = -3 + 5 - 2 = 0
f(−1) = 0.
b) Известно, что график функции проходит через точку ( k ; 0). Найдите значение k.
у = -3х² - 5х - 2 х=k у=0
-3k² - 5k - 2 = 0/-1
3k² + 5k + 2 = 0, квадратное уравнение, ищем корни:
D=b²-4ac =25 - 24 = 1 √D= 1
k₁=(-b-√D)/2a
k₁=(-5-1)/6
k₁= -6/6
k₁= -1;
k₂=(-b+√D)/2a
k₂=(-5+1)/6
k₂= -4/6
k₂= -2/3.
3. Дана функция у = 2х² − 8x + 7.
Не строя графика, найдите:
а) область определения функции.
1) Область определения функции - это значения х, при которых функция существует.
Так как график квадратичной функции парабола, область её определения ничем не ограничен.
Область определения функции D(y) = х∈R, множество всех действительных чисел, или D(y) = х∈(-∞; +∞).
b) наименьшее значение функции.
Наименьшее и наибольшее значение функции определяется ординатой вершины параболы в зависимости от направления её ветвей.
В данном примере ветви параболы направлены вверх, значит, наименьшим значением функции будет ордината вершины (у₀).
у = 2х² − 8x + 7
Сначала найти х₀:
х₀ = -b/2a
х₀ = 8/4 = 2;
у₀ = 2 * 2² - 8*2 + 7 = 8 - 16 + 7 = -1.
у наим. = -1.