
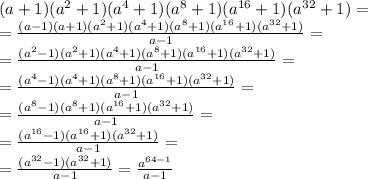
Объяснение:
В основе метода математической индукции (ММИ) лежит принцип математической индукции: утверждение $P(n)$ (где $n$ - натуральное число) справедливо при $\forall n \in N$, если:
Утверждение $P(n)$ справедливо при $n=1$.
Для $\forall k \in N$ из справедливости $P(k)$ следует справедливость $P(k+1)$.
Доказательство с метода математической индукции проводится в два этапа:
База индукции (базис индукции). Проверяется истинность утверждения при $n=1$ (или любом другом подходящем значении $n$)
Индуктивный переход (шаг индукции). Считая, что справедливо утверждение $P(k)$ при $n=k$, проверяется истинность утверждения $P(k+1)$ при $n=k+1$.
Метод математической индукции применяется в разных типах задач:
Доказательство делимости и кратности
Доказательство равенств и тождеств
Задачи с последовательностями
Доказательство неравенств
Нахождение суммы и произведения
по примеру реши.
x^3 - 6x^2 + 11x - 6 = 0 можно, конечно, решить формулой кардано для решения кубических уравнений, но это долго и трудно. проще подобрать корни схемой горнера. возможные рациональные корни x = a/b, где а - делитель свободного члена, b - делитель старшего коэффициента. x = 1, -1, 2, -2, 3, -3, 6, -6 находишь значения в этих точках. y(1) = 1 - 6 + 11 - 6 = 0 - повезло сразу! теперь раскладываем: x^3 - x^2 - 5x^2 + 5x + 6x - 6 = 0 (x - 1)(x^2 - 5x + 6) = 0 (x - 1)(x - 2)(x - 3) = 0 ответ: x1 = 1, x2 = 2, x3 = 3