
рассмотрим наше уравнение:
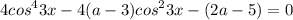
выполним замену cos²3x=t; t≥0
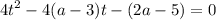
чтобы уравнение имело хотя бы один корень надо чтобы D≥0
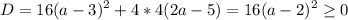
Это неравенство выполняется для любых a
тогда проверим корни, необходимо чтобы t≥0
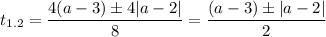
рассмотрим первый корень
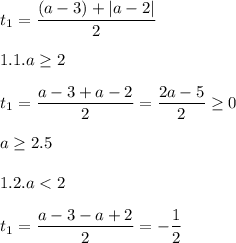
значит при а≥2.5 мы получим один положительный корень (относительно t)
проверим второй корень
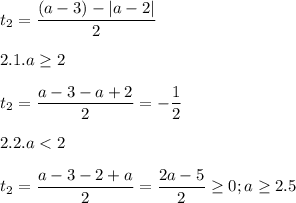
тут положительных корней не получим.
значит рассмотрим один положительный корень t=(2a-5)/2. при а≥2,5
выполним обратную замену
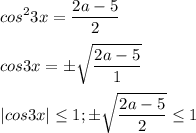
рассмотрим положительный корень
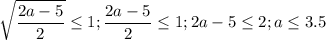
рассмотрим отрицательный корень
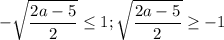
выполняется для всех а≥2.5
Собираем все вместе 2,5≤а≤3,5
75
Объяснение:
следующий член больше за предидущий на 8