
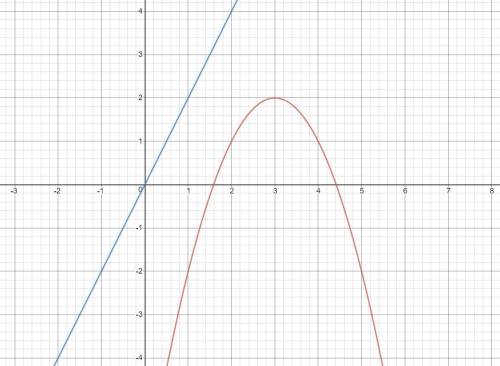
Строим графики функций. y=-x²+6x-7 - парабола с ветвями вниз. y=2x+a - прямая y=2x, которая перемещается вдоль оси Oy в зависимости от значения a (картинка 1).
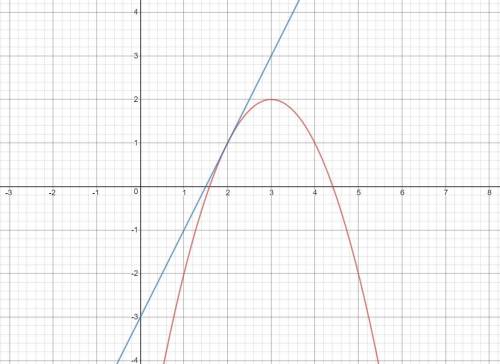
При некотором a прямая будет касательной к параболе (картинка 2). В таком случае уравнение -x²+6x-7=2x+a будет иметь один корень, что соответствует нулевому дискриминанту.
-x²+6x-7=2x+a ⇒ x²-4x+7+a=0
D=16-4(7+a)=16-28-4a=-4a-12 ; -4a-12=0 ⇒ a=-3
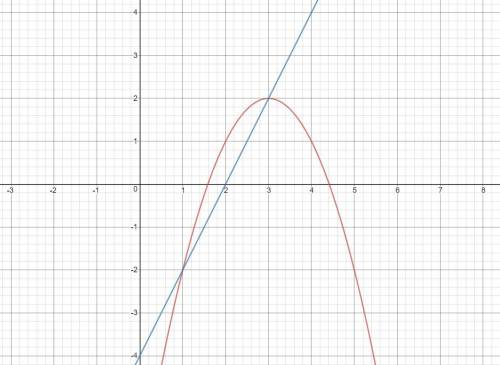
При меньших a прямая будет пересекать параболу в двух точках (картинка 3). Получим окончательный ответ a∈(-∞; -3]
ответ: a∈(-∞; -3]
1.a)При возведении степени в степень показатели степеней перемножаются:
(a³)⁴=a¹² (t²)⁵=t¹⁰ (n⁶)⁸=n⁴⁸ (u⁵)⁷=u³⁵ (u⁹)³=u²⁷ (k¹¹)⁴=k⁴⁴
b)Когда двойные скобки, сначала возвести в степень первую скобку, потом вторую:
6(h⁷)⁴=6h²⁸ -2(y⁵)⁶= -2y³⁰ -(d³)⁵= -d¹⁵ ((-2)⁴)²=16²=256
((-3)²)²=9²=81 ((-5)²)²=25²=625
6. При возведении в степень произведения чисел каждый множитель возводится в степень отдельно.
При возведении в степень дроби числитель и знаменатель возводятся в одну и ту же степень:
(ab)⁵=a⁵b⁵
(xyz)⁴=x⁴y⁴z⁴
(-tyu)⁶=t⁶y⁶u⁶
(2n)⁴=2⁴n⁴=16n⁴
(-3xy)³= -3³x³y³= -9x³y³
(0,1cd)²=0,1²c²d²=0,01c²d²
(-1/2sr)⁵= -1⁵/2⁵s⁵r⁵=-1/32s⁵r⁵
(1/3mn)²=1²/3²m²n²=1/9m²n²
Уравнение касательной к графику функции в точке имеет вид:
имеет вид:  .
.
Итак, для начала высчитаем . Чтобы сделать это, просто подставим в нашу функцию вместо
. Чтобы сделать это, просто подставим в нашу функцию вместо  значение
значение  .
.
Теперь найдём производную этой функции.
Теперь вычислим . То же самое - подставляем в производную вместо
. То же самое - подставляем в производную вместо  значение
значение  .
.
Теперь вернёмся к уравнению касательной, написанному выше, и подставим туда вычисленные величины.