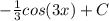Если это задача из школьной программы, то ее можно решить так:
О—орел
Р— решка
Возможные варианты при бросании трижды:
1) О О О
2) О О Р
3) О Р О
4) Р О О
5) О Р Р
6) Р Р О
7) Р О Р
8) Р Р Р
Всего 8 исходов
Благоприятных исходов: 3 (выпало ровно две решки)
Вероятность равна: р=3/8=0,375
ответ: 0,375
Если из высшей математики, то лучше по формуле Бернулли:
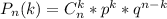
k=2 —количество наступления нужного события
n=3 — количество испытаний
p=0,5 — вероятность наступления события (появление решки)
q=1-p=1-0,5=0,5 — вероятность противоположного события (выпадение орла)
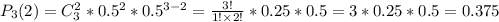
ответ: 0,375
Я не стану спецом лезть в инет и чекать где она применяется, я лишь приведу свои примеры, где тригонометрия мне пригодилась, да они будут тупыми, но все же :D
Во-первых, без тригонометрии очень сложно в физике, при решении сложных физических задач на механику, электродинамику очень часто приходится знать тригонометрию, особенно в теме колебательного движения, так как гармонические колебания происходят по закону синуса или косинуса, то есть графиком будет синусоида.
Во-вторых, когда тебе может быть скучно, допустим ты находишься в своей машине на горке под определенным углом к горизонту и тебе нужно найти проекцию силы тяжести, которая тянет твою машину вниз, то без тригонометрии тоже сложно это сделать. Ну это все шутки конечно...
Тригонометрия нужна в разработке 3-D игр, даже не зачем объяснять почему - это итак очевидно, нужно, допустим, определить траекторию полета какого-то тела или проверить столкнутся ли тела, либо тебе необходимо заставить объект двигаться в любом направлении - это все без так называемых "синусов" и "косинусов" не сделать.
Вообщем говоря стоит признать уже всем, что без тригонометрии нам никуда и как ни крути все равно придется ее знать.
1) lg11-lg110=lg11-lg(11*10)=lg11-(lg11+lg10)=lg11-lg11-lg10=-1
2) sin^4a-cos^4a+cos^2a
По формулам понижения степени:
Подставляем и получаем:
Приводим подобные и все под общий знаменатель и получаем:
3)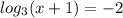
Найдем область определения:
х+1>0, т.е х>-1
Теперь решаем:
По определению логарифма получаем:
Решение лежит в области определения, значит оно удовлетворяет уравнению
4) Найти область определения функции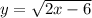
Чтобы функция была определена на множестве действительных чисел R, необходимо чтобы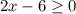 что эквивалентно неравенству
что эквивалентно неравенству 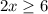 , или
, или 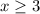
Область определения функции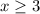
5) Найти период функции. По определению периода:
T-называется периодом функции F(x), если F(x+T)=F(x)
Подставим в нашу функцию:
Нам известно, что период функции cos(x)=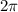
Т.е приходим к такому уравнению относительно Т:
6) Первообразная от функции является неопределенным интегралом, значит надо вычислить
Сделаем простую замену u=3x, du=3dx отсюда dx=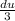 , в итоге получаем:
, в итоге получаем:
Вернемся к исходным переменным и получим:
ответ: Первообразная от функции y=sin(3x) будет равна